量子力学のハミルトニアン\(\hat{H}\)は次のように表された。
$$iħ\frac{∂}{∂t}Ψ({\bf r},t)=\left( -\frac{ħ^2}{2m}∇^2 +V({\bf r}) \right) Ψ({\bf r},t)$$
$$iħ\frac{∂}{∂t}Ψ({\bf r},t)=\hat{H}Ψ({\bf r},t)$$
参考:シュレディンガー方程式と運動量演算子の求め方
この記事では、極座標のラプラシアンから、極座標のシュレディンガー方程式とハミルトニアンを求める。
なお、水素原子のまわりの電子や球面調和関数の導出などについては別の記事にまとめてあります。
参考:水素原子中の電子の波動関数と球面調和関数の導出
前提知識
極座標のナブラ
\begin{eqnarray} ∇&=&{\bf e}_x\frac{∂}{∂x}+{\bf e}_y\frac{∂}{∂y}+{\bf e}_z\frac{∂}{∂z}\\&=&{\bf e}_r\frac{∂}{∂r}+\frac{{\bf e}_θ}{r}\frac{∂}{∂θ}+\frac{{\bf e}_φ}{rsinθ}\frac{∂}{∂φ} \end{eqnarray}
極座標のラプラシアン
\begin{eqnarray} ∆&=&∇^2=\left( {\bf e}_r\frac{∂}{∂r}+\frac{{\bf e}_θ}{r}\frac{∂}{∂θ}+\frac{{\bf e}_φ}{rsinθ}\frac{∂}{∂φ} \right) \left( {\bf e}_r\frac{∂}{∂r}+\frac{{\bf e}_θ}{r}\frac{∂}{∂θ}+\frac{{\bf e}_φ}{rsinθ}\frac{∂}{∂φ} \right)\\&=&\frac{∂^2}{∂r^2}+\frac{2}{r}\frac{∂}{∂r}+\frac{1}{r^2} \left( \frac{1}{sinθ}\frac{∂}{∂θ} \left( sinθ\frac{∂}{∂θ} \right) +\frac{1}{sin^2θ}\frac{∂^2}{∂φ^2} \right)\\&=&\frac{1}{r^2}\frac{∂}{∂r}\left( r^2 \frac{∂}{∂r} \right)+\frac{1}{r^2} \left( \frac{1}{sinθ}\frac{∂}{∂θ} \left( sinθ\frac{∂}{∂θ} \right) +\frac{1}{sin^2θ}\frac{∂^2}{∂φ^2} \right) \end{eqnarray}
極座標の単位ベクトル
$${\bf e}_r=(sinθcosφ,sinθsinφ,cosθ)$$
$${\bf e}_θ=(cosθcosφ,cosθsinφ,-sinθ)$$
$${\bf e}_φ=(-sinφ,cosφ,0)$$
角運動量演算子
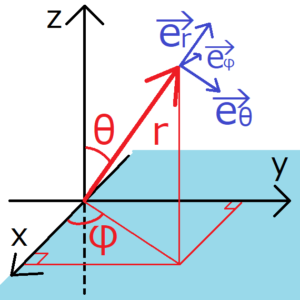
古典的な角運動量は\({\bf l}={\bf r}×{\bf p}\)だから、角運動量演算子\(\hat{ \bf l }\)は、運動量演算子と極座標のナブラを使って次のように変形できる。\({\bf A}×{\bf A}={\bf 0}\)と外積の符号に注意する。右ねじを意識すれば、外積の向きは間違えないはずだ。
参考:力のモーメントと角運動量の関係
\begin{eqnarray} \hat{ \bf l }&=&\hat{ \bf r }×\hat{ \bf p }\\&=&{\bf r}×\frac{ħ}{i}∇\\&=&r{\bf e}_r×\frac{ħ}{i}\left( {\bf e}_r\frac{∂}{∂r}+\frac{{\bf e}_θ}{r}\frac{∂}{∂θ}+\frac{{\bf e}_φ}{rsinθ}\frac{∂}{∂φ} \right)\\&=&\frac{ħ}{i}\left( r({\bf e}_r×{\bf e}_r)\frac{∂}{∂r}+({\bf e}_r×{\bf e}_θ)\frac{∂}{∂θ}+({\bf e}_r×{\bf e}_φ)\frac{1}{sinθ}\frac{∂}{∂φ} \right)\\&=&\frac{ħ}{i}\left( ({\bf e}_r×{\bf e}_θ)\frac{∂}{∂θ}+({\bf e}_r×{\bf e}_φ)\frac{1}{sinθ}\frac{∂}{∂φ} \right)\\&=&\frac{ħ}{i}\left( (+{\bf e}_φ)・\frac{∂}{∂θ}+(-{\bf e}_θ)・\frac{1}{sinθ}\frac{∂}{∂φ}\right) \end{eqnarray}
次に、この角運動量演算子の二乗\(\hat{\bf l}^2\)を考える。極座標の単位ベクトル\({\bf e}_r,{\bf e}_φ,{\bf e}_θ\)はそれぞれ直交し、かつその大きさは\(1\)である。だから、\({\bf e}_φ\)と\({\bf e}_θ\)の内積について、次の関係が成り立つ。
$${\bf e}_φ・{\bf e}_φ=1 \quad {\bf e}_θ・{\bf e}_θ=1$$
この関係を意識して\(\hat{\bf l}^2\)を計算する。
\begin{eqnarray} \hat{ \bf l }^2&=&\left( \frac{ħ}{i} \right)^2 \left( {\bf e}_φ・\frac{∂}{∂θ}-{\bf e}_θ・\frac{1}{sinθ}\frac{∂}{∂φ}\right) \left( {\bf e}_φ・\frac{∂}{∂θ}-{\bf e}_θ・\frac{1}{sinθ}\frac{∂}{∂φ}\right)\\&=&-ħ^2\left( \frac{∂^2}{∂θ^2}-{\bf e}_φ・\frac{∂}{∂θ} \left( {\bf e}_θ・\frac{1}{sinθ} \right) \frac{∂}{∂φ}-\frac{{\bf e}_θ}{sinθ} \left( \frac{∂}{∂φ}{\bf e}_φ \right) \frac{∂}{∂θ}+ \frac{1}{sin^2θ}\frac{∂^2}{∂φ^2}\right)・・・(1) \end{eqnarray}
第二項の計算
上の式のカッコ内の第二項を詳しく計算してみる。
まず、内積\({\bf e}_φ・{\bf e}_θ\)は、
\begin{eqnarray} {\bf e}_φ・{\bf e}_θ&=&-sinφcosθcosφ+cosφcosθsinφ\\&=&0 \end{eqnarray}
また、\({\bf e}_θ\)を\(θ\)で偏微分すると、
$$ \frac{∂{\bf e}_θ}{∂θ}=(-sinθcosφ,-sinθsinφ,-cosθ) $$
だから、内積\({\bf e}_φ・\frac{∂{\bf e}_θ}{∂θ}\)は、
\begin{eqnarray} {\bf e}_φ・\frac{∂{\bf e}_θ}{∂θ}&=&sinφsinθcosφ-cosφsinθsinφ\\&=&0 \end{eqnarray}
以上を使うと、第二項が計算できる。
\begin{eqnarray} -{\bf e}_φ・\frac{∂}{∂θ} \left( {\bf e}_θ・\frac{1}{sinθ} \right) \frac{∂}{∂φ}&=&-{\bf e}_φ \left( \frac{1}{sinθ}\frac{∂{\bf e}_θ}{∂θ}+{\bf e}_θ\frac{∂}{∂θ}\frac{1}{sinθ} \right) \frac{∂}{∂φ}\\&=&-\left( \frac{1}{sinθ}{\bf e}_φ・\frac{∂{\bf e}_θ}{∂θ}+{\bf e}_φ・{\bf e}_θ\frac{∂}{∂θ}\frac{1}{sinθ} \right) \frac{∂}{∂φ}\\&=&0 \end{eqnarray}
第三項の計算
次に、カッコ内の第三項を詳しく計算してみる。
単位ベクトル\({\bf e}_φ\)を\(φ\)で偏微分すると、
$$ \frac{∂{\bf e}_φ}{∂φ}=(-cosφ,-sinφ,0)$$
だから、内積\({\bf e}_θ・\frac{∂{\bf e}_φ}{∂φ}\)も次のように求められる。
\begin{eqnarray} {\bf e}_θ・\frac{∂{\bf e}_φ}{∂φ}&=&-cosθcos^2φ-cosθsin^2φ\\&=&-cosθ(cos^2φ+sin^2φ)\\&=&-cosθ \end{eqnarray}
最終的な\(\hat{\bf l}^2\)
求めた第二項と第三項を、元の式(1)に代入する。
\begin{eqnarray} \hat{ \bf l }^2&=&-ħ^2\left( \frac{∂^2}{∂θ^2}-{\bf e}_φ・\frac{∂}{∂θ} \left( {\bf e}_θ・\frac{1}{sinθ} \right) \frac{∂}{∂φ}-\frac{{\bf e}_θ}{sinθ} \left( \frac{∂}{∂φ}{\bf e}_φ \right) \frac{∂}{∂θ}+ \frac{1}{sin^2θ}\frac{∂^2}{∂φ^2}\right)\\&=&-ħ^2\left( \frac{∂^2}{∂θ^2}+0-\frac{-cosθ}{sinθ} \frac{∂}{∂θ}+ \frac{1}{sin^2θ}\frac{∂^2}{∂φ^2}\right)\\&=&-ħ^2\left( \frac{∂^2}{∂θ^2}+\frac{cosθ}{sinθ} \frac{∂}{∂θ}+ \frac{1}{sin^2θ}\frac{∂^2}{∂φ^2}\right)\\&=&-ħ^2\left( \frac{1}{sinθ} \left( sinθ \frac{∂^2}{∂θ^2}+(sinθ)’\frac{∂}{∂θ} \right)+\frac{1}{sin^2θ}\frac{∂^2}{∂φ^2}\right)\\&=&-ħ^2\left( \frac{1}{sinθ} \frac{∂}{∂θ} \left( sinθ \frac{∂}{∂θ} \right)+\frac{1}{sin^2θ}\frac{∂^2}{∂φ^2}\right) \end{eqnarray}
\(\hat{\bf l}^2\)がこのように変形できるということは、この\(\hat{\bf l}^2\)を極座標のラプラシアン\(∆\)に組み込めることを意味する。
\begin{eqnarray} ∆&=& \frac{1}{r}\frac{∂^2}{∂r^2}r+\frac{1}{r^2} \left( \frac{1}{sinθ}\frac{∂}{∂θ} \left( sinθ\frac{∂}{∂θ} \right) +\frac{1}{sin^2θ}\frac{∂^2}{∂φ^2} \right)\\&=&\frac{1}{r}\frac{∂^2}{∂r^2}r-\frac{\hat{\bf l}}{ħ^2r^2} \end{eqnarray}
この記事の一番最初にあるシュレディンガー方程式の\(∇^2\)に、このラプラシアン\(∆\)を代入する。
\begin{eqnarray} iħ\frac{∂}{∂t}Ψ&=&\left( -\frac{ħ^2}{2m}∇^2 +V({\bf r}) \right) Ψ\\&=&\left( -\frac{ħ^2}{2m} \left( \frac{1}{r}\frac{∂^2}{∂r^2}r-\frac{\hat{\bf L}}{ħ^2r^2} \right) +V({\bf r}) \right)Ψ\\&=&\left( \frac{1}{2m} \left( \frac{ħ}{i} \right)^2 \left( \frac{1}{r}\frac{∂^2}{∂r^2}r \right) +\frac{\hat{\bf l}}{2mr^2} +V({\bf r}) \right)Ψ \end{eqnarray}
エルミートな動径方向の運動量演算子\(\hat{p}_r≡\frac{ħ}{i}\frac{1}{r}\frac{∂}{∂r}r\)を導入すると、このシュレディンガー方程式は次の形になる。
$$iħ\frac{∂}{∂t}Ψ=\left( \frac{\hat{p}_r^2}{2m} +\frac{\hat{\bf l}}{2mr^2} +V({\bf r}) \right)Ψ $$
以上で、極座標のシュレディンガー方程式が求められた。
この方程式から、極座標のハミルトニアン\(\hat{H}\)は、次のように表現される。
$$\hat{H}=\frac{\hat{p}_r^2}{2m} +\frac{\hat{\bf l}}{2mr^2} +V({\bf r})$$
ハミルトニアンの各項の意味
\(\frac{\hat{p}_r^2}{2m}\)は動径方向の運動エネルギー、\(\frac{\hat{\bf l}}{2mr^2}\)は回転運動エネルギー、\(V({\bf r})\)はポテンシャルエネルギーを表している。
まとめ
3次元の極座標におけるシュレディンガー方程式とハミルトニアンを求めた。
参考文献
・A.メシア(1972)『メシア量子力学 2』(小出昭一郎・田村二郎訳),東京図書株式会社.
・猪木慶治・川合光(1994)『量子力学I』,講談社.



