\({\bf A}=(a_x,a_y,a_z)\)、\({\bf B}=(b_x,b_y,b_z)\)
内積
\begin{eqnarray} {\bf A}・{\bf B}&=&a_xb_x+a_yb_y+a_zb_z\\&=&|{\bf A}||{\bf B}|cosθ \end{eqnarray}
外積
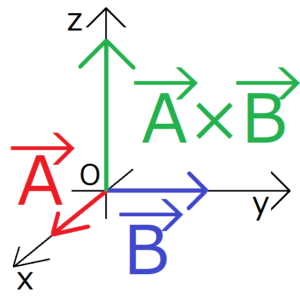
右ねじを意識すれば外積の向きを間違えない。
\begin{eqnarray} {\bf A}×{\bf B}&=&\begin{vmatrix} {\bf i}&{\bf j}&{\bf k}\\a_x&a_y&a_z\\b_x&b_y&b_z \end{vmatrix}\\&=&{\bf i}(a_yb_z-a_zb_y)+{\bf j}(a_zb_x-a_xb_z)+{\bf k}(a_xb_y-a_yb_x) \end{eqnarray}
$$|{\bf A}×{\bf B}|=|{\bf A}||{\bf B}|sinθ$$
参考:行列式の計算方法
内積の用途
平面波の記述
次のように表せる波\(ψ(x,t)\)を考える。
$$ψ(x,t)=Acos(kx-ωt)$$
\(A\)は振幅、\(k\)は波数(単位長さあたりの波の数)、\(ω\)は角振動数を表す。
これを3次元に拡張すると、次のようになる。
$$ψ({\bf r}, t)=Acos({\bf k}・{\bf r}-ωt)$$
\({\bf k}\)は波数ベクトルである。このベクトルは波の進行方向を向いている。
この波の式は、波数ベクトルの方向に、一定間隔で波が現れることを表している。このような波を平面波という。
ブラベクトルとケットベクトル
量子力学では、ブラベクトル\(<u|\)とケットベクトル\(|v>\)をよく使う。
$$<u|=\left( u_1 , u_2 , \ldots \right)$$
$$|v>=\left( \begin{array}{c} v_1 \\ v_2 \\ \vdots \end{array} \right)$$
これを\(<u|v>\)のように並べてみる。
\begin{eqnarray} <u|v>&=&\left( u_1 , u_2 , \ldots \right)\left( \begin{array}{c} v_1 \\ v_2 \\ \vdots \end{array} \right) \\&=&u_1v_1+u_2v_2+\ldots \end{eqnarray}
この式から、\(<u|v>\)は内積を表していることがわかる。
外積の用途
角運動量の定義
角運動量とは、回転運動の勢いや激しさを表すパラメータで、\({\bf L}\)で表される。高校物理で学習した運動量\({\bf p}\)は並進運動に関するものだが、角運動量はこれの回転運動バージョンだと考えれば考えやすいだろう。
位置\({\bf r}\)と運動量\({\bf p}\)を使って、角運動量\(L\)は次のように定義される。
$${\bf L}={\bf r}×{\bf p}$$
力のモーメントの定義
高校物理で習った力のモーメント\(N\)も、実は外積で定義される。
$${\bf N}={\bf r}×{\bf F}$$
詳しくは下の記事を参照のこと。

