[mathjax]
カルノーサイクルとは、等温過程と断熱過程という準静的過程で構成された可逆サイクルのことである。前の記事では、このサイクルの熱効率\(η\)を求めた。
今回の記事では、カルノーサイクルを使って、可逆サイクルの熱効率の方が、不可逆サイクルの熱効率よりも大きいことを示す。
カルノーサイクルと任意のサイクル
両サイクルの熱量・仕事が満たす関係式
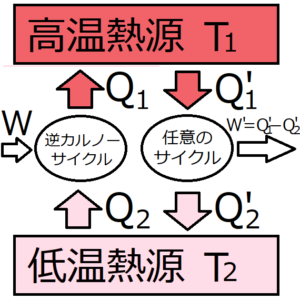
高熱源から熱\(Q’_1\)を受け取って仕事\(W’\)と熱\(Q_2\)を出力するサイクル\(C’\)と、逆カルノーサイクル\(C\)を並べる。サイクル\(C’\)は可逆でも不可逆でもよい。
ここで、\(Q_2=Q’_2\)として、さらにこの2つのサイクルを1つのサイクルとしてみなすと、上図を次のように描きなおせる。
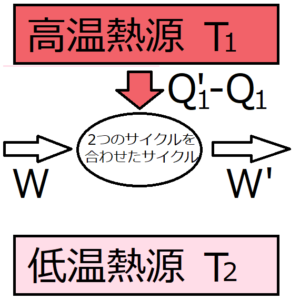
サイクル全体では、熱量\(Q’_1-Q_1\)を受け取って、仕事\(W’-W\)を出力する。したがって、次の式が成り立つ。
ところが、もし\(Q’_1-Q_1>0\)ならば、このサイクルは受け取った熱量をすべて仕事に変換していることになるため、トムソンの原理に矛盾する。したがって、熱量に関して次の式が成り立つ。
$$Q’_1-Q_1≤0$$
\(Q_1\)を右辺に移項する。
$$Q’_1≤Q_1$$
この式と式(1)より、
$$W’_1≤W_1$$
2つのサイクルの熱効率について
熱効率の定義は、\(η=(出力する仕事)/(受け取った熱量)\)であった。
この定義に沿って、任意のサイクルの熱効率\(η’\)とカルノーサイクルの熱効率\(η_C\)の差を求める。\(Q_2=Q’_2\)と\(Q’_1≤Q_1\)に気を付ける。
$$η’≤η_C$$
この式は、カルノーサイクルの熱効率\(η_C\)が、あらゆるサイクルの中で最大となることを表している。
任意のサイクルが可逆のときに、等号が成立する。
まとめ
・あらゆるサイクルの熱効率が、カルノーサイクルの熱効率を超えないことを確認した。
参考文献
・三宅哲(1994)『熱力学』,裳華房.

