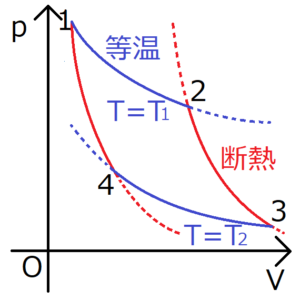
カルノーサイクルとは、等温過程と断熱過程という2種類の準静的過程で構成された熱機関のことである。
この記事では、このサイクルにおける仕事と熱効率の導出を行う。
また、この記事内では、前の記事で求めた公式をたくさん使うことになる。もし自信がなかったら、先に下の記事を読んでおくことをお勧めする。また、断熱過程のグラフの方が等温過程のグラフよりも急である理由も、下の記事を参照のこと。
目次
カルノーサイクルの過程
上図のカルノーサイクルは、4つの過程で成り立っている。それぞれで系にどのような影響が表れるか、個別に確かめていく。
1→2等温過程
等温過程における系がする仕事\(W’\)は、次のように表された。
$$W’_{1→2}=nRTln\frac{V_2}{V_1}$$
ジュールの法則より、理想気体において、温度\(T\)が一定ならば、内部エネルギーは体積によらず一定である。つまり、\(dU=0\)
これらを熱力学第一法則\(dU=d’Q-d’W’\)に代入する。温度は\(T_1\)で一定である。
$$Q_{1→2}=nRT_1ln\frac{V_2}{V_1}$$
この式から、\(Q_{1→2}>0\)がいえる。つまり、この等温過程によって、系に熱が取り込まれていることがわかる。
2→3断熱過程
断熱過程より、\(d’Q=0\)である。これを熱力学第一法則に代入する。
$$dU=-d’W’=-pdV$$
\(C_V\)を1molあたりの定積熱容量(定積モル比熱)とすると、
$$dU=nC_VdT$$
この2式より、
$$pdV=-nC_VdT$$
\(d’W’=pdV\)の両辺を積分して計算する。
3→4等温過程
1→2のときと同様の計算をするが、\(V_3>V_4\)に注意すること。
$$W’_{3→4}=-nRT_2ln\frac{V_3}{V_4}$$
等温過程とジュールの法則より、
$$dU=0$$
これらを熱力学第一法則\(dU=d’Q-d’W’\)に代入する。温度は\(T_2\)で一定である。
$$Q_{3→4}=-nRT_2ln\frac{V_3}{V_4}$$
この式から、\(d’Q<0\)がいえる。つまり、この等温過程によって、系から熱が放出されていることがわかる。
4→1断熱過程
2→3の断熱過程と同様にして求める。
カルノーサイクルの仕事
カルノーサイクルが1→2→3→4→1というようにして一周する間に気体がした仕事\(W’\)を求める。
断熱過程の式について
2→3は断熱過程だから、\(T_1V_2^{γ-1}=T_2V_3^{γ-1}\)が成立。
4→1も同様に、\(T_1V_1^{γ-1}=T_2V_4^{γ-1}\)が成立。
上の式を下の式で割ると、
$$\frac{V_2}{V_1}=\frac{V_3}{V_4}$$
断熱過程の式の導入
上の式を仕事の式に代入すると、
\(T_1>T_2\)に注意すると、\(W’>0\)を確認できる。ちなみにこの\(W’\)の値は、上図の赤線と青線に囲まれた面積に等しい。
カルノーサイクルの熱量
気体がカルノーサイクル1→2→3→4→1一周分で得る熱量\(Q\)は、
これは、気体がした仕事\(W’\)と等しい。
$$Q=W’$$
この式と熱力学第一法則より、カルノーサイクルが一周すると、内部エネルギーが元通りになることが確認できる。
カルノーサイクルの熱効率
熱効率とは
熱効率\(η\)とは、サイクルに入れる熱量と、サイクルが外部にする仕事の割合である。次のように定義される。
$$η=\frac{W_{out}}{Q_{in}}$$
カルノーサイクルでは、一周すると元の状態に戻ってくるから、\(dU=0\)となる。すると熱力学第一法則より、\(W_{out}=Q_{in}-Q_{out}\)が求まる。これを熱効率の定義に代入する。
$$η=1-\frac{Q_{out}}{Q_{in}}$$
この式の導出には理想気体の状態方程式が使われていないため、サイクル内の気体が理想気体でなくても成り立つ。
理想気体のカルノーサイクルの熱効率
今考えている理想気体のカルノーサイクルでは、サイクルに入れる熱量は\(Q_{1→2}\)である。
まとめ
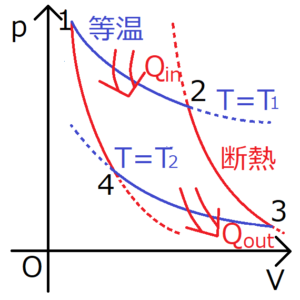
・カルノーサイクルは、等温過程と断熱過程で構成される。
・カルノーサイクルの効率\(η\)は、
一般的な気体:\(η=1-\frac{Q_{out}}{Q_{in}}\)
理想気体:\(η=1-\frac{T_2}{T_1}\)
参考文献
・三宅哲(1994)『熱力学』,裳華房.

