換算質量\(μ\)を導入することで、質量がそれぞれ\(m_1,m_2\)である2体の運動を、質量\(μ\)の1体の運動として考えることができる。この換算質量\(μ\)は、次の式を満たす。
この記事では、重心周りの運動エネルギーから換算質量を求めてみる。
目次
運動エネルギーから換算質量を求める
相対座標と重心
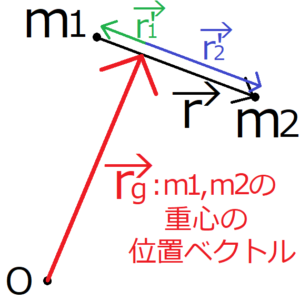
質量がそれぞれ\(m_1,m_2\)の質点が存在する。2つの質点の重心の位置ベクトルを\({\bf r}_g\)、その重心から質点\(m_1,m_2\)へ向かうベクトルをそれぞれ\({\bf r}’_1,{\bf r}’_2\)とする。これら\({\bf r}’_1,{\bf r}’_2\)は、それぞれ重心\({\bf r}_g\)に対する質点\(m_1,m_2\)の位置を表しているため、質点\(m_1,m_2\)の相対座標とよぶ。
さらに、\(m_1\)から\(m_2\)へ向かうベクトルを\(\bf r\)とする。質点\(m_1,m_2\)の位置ベクトルをそれぞれ\({\bf r}_1,{\bf r}_2\)とおくと、質点\(m_1\)に対する質点\(m_2\)の相対座標\({\bf r}\)は、次のように表される。
また、復習になるが、重心を質量などを使って表すと、次のようになった。
全体の運動エネルギー
2つの質点の運動エネルギーの和\(T\)は、重心の運動エネルギー\(T_g\)と、2つの質点の重心に対する運動エネルギーの和\(T’\)を足したものとなる。この証明は、この記事の最後に補足として示した。
$$T=T_g+T’$$
そして、\(T_g\)と\(T’\)はそれぞれ次のようになる。
重心周りの運動エネルギー\(T’\)と換算質量\(μ\)
重心の位置ベクトル\({\bf r}_g\)とベクトル\({\bf r}’_1,{\bf r}’_2\)の大きさの比に注目すると、これらの間には、それぞれ次の関係が成り立つ。\({\bf r}’_1\)は\({\bf r}\)に対して逆向きになっているから、マイナスをつける必要がある。
これらを\(T’\)の式に代入する。
ここで、換算質量を\(μ≡\frac{m_1m_2}{m_1+m_2}\)と定義する。
この式は、2つの質点の重心に対する運動エネルギーの和\(T’\)と、質点\(m_1\)を固定して、なおかつ質点\(m_2\)の質量を\(μ\)とみなしたときの、質点\(μ\)の質点\(m_1\)に対する運動エネルギーが等しいことを意味する。
ちなみに、換算質量の定義式を変形すると、次の関係が求まる。
補足:\(T=T_g+T’\)の証明
全体の運動エネルギー\(T\)は、重心の運動エネルギー\(T_g\)と、重心周りの運動エネルギーの和\(T’=\sum_{j=1}^nT’_j\)で表せることを示す。
原点に対する\(j\)番目の質点\(m_j\)の位置\({\bf r}_j\)を、重心の位置\({\bf r}_g\)と重心に対する質点の相対座標\({\bf r}’_j\)を使って表すと、次のようになる。
あらゆる物体は質点の集合体としてみなせる。今考える物体が\(n\)個の質点で成り立っているとして、さらに物体全体の質量を\(M\)とおくと、\(M{\bf r}_g\)は次のように変形できる。
この式の最初と最後を比較すると、次の関係が求まる。
質点が時間に依存しないため、この式の時間微分は、
粒子全体の運動エネルギー\(T\)の変形
質量\(m_j\)の質点の位置ベクトルは\({\bf r}_j\)だから、この質点の運動エネルギー\(T_j\)は、次のようになる。
\(n\)個の質点の運動エネルギーの和\(T\)を変形してみる。
ただし、最後の変形で式(1)を使った。
式(2)の各項の考察
式(2)の最後の式の第一項は、物体全体の質量がすべて重心に集中したときの、重心の運動エネルギー\(T_g\)を表している。そして第二項は、それぞれの粒子の重心に対する運動エネルギーの和\(T’\)を表している。
つまり、粒子全体の運動エネルギー\(T\)は、重心の運動エネルギー\(T_g\)とすべての質点の重心に対する運動エネルギー\(T’\)の和に等しくなる。
まとめ
・重心周りの運動エネルギーから換算質量を求めた。
参考文献
・Goldstein, Herbert. “Classical Mechanics (World Student)” 2nd ed. Reading, Mass: Addison-Wesley Publishing Company, 1980.
(題名を斜体にできないので” “でくくっています)
・戸田盛和(1982)『力学 (物理入門コース1)』,岩波書店.

