電流とは、正の電荷の流れを表す量のことである。この記事では、導体中を流れる電荷から電流の定義を考えた後、電荷保存則について考える。
電流と電流密度の定義
電流とは
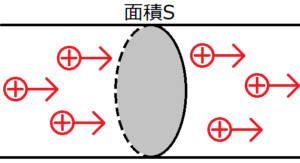
上の図では、導体中を正電荷が移動している様子を表している。この場合、導体を流れる電流\(I\)の大きさは、単位時間で導体の断面積\(S\)を垂直に通過する電荷\(Q\)で定義される。
ただし、実際は陽子よりも電子のほうがはるかに質量が小さいため、負の電荷のほうが移動しやすい。電子の進行方向と電流の向きが逆になっているのは、最初に正の電荷の進行方向によって電流の向きを定義してしまったからである。
電流密度とは
電流密度\(i\)とは、単位面積あたりに流れる電流の大きさのことを指す。
つまり、電流密度を導体の断面で面積分すれば、導体に流れる電流\(I\)を求められる。
電流の連続の式と電荷保存則
上の電流密度の式を使うと、量子力学の確率流密度や流体力学でも出てくる連続の式が求まる。また、電磁気学における連続の式は電荷保存則と呼ばれるのだが、なぜそう呼ばれるのかも考える。
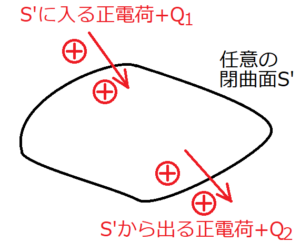
閉曲面に入ってくる正電荷を\(Q_1\)、出ていく正電荷を\(Q_2\)とする。\(Q_1<Q_2\)とすると、閉曲面全体では電荷は減少することになる。
また、電荷\(Q\)は、電荷密度\(ρ\)の体積積分で与えられた。
参考:ガウスの法則の導出
式(1)の左辺の電流\(I\)に電流密度の式を、右辺の\(Q\)に上の電荷密度の式を代入する。ただし、閉曲面\(S\)に囲まれた部分の体積を\(V\)とおく。
上の最後の式は、閉曲面\(S\)内の電荷量の時間変化を表す。
ここで、電流密度のベクトル\({\bf i}\)の向きは当然正電荷が進む向きを表している。
この式の左辺にガウスの定理を導入する。
式(3)を、式(2)に代入する。
両辺の体積積分を外しても等式は成り立つから、
この式が電流の連続の式である。
定常電流
定常電流とは、電流の大きさと向きが変化しないような電流を指す。定常電流が閉曲面を通過する場合は、閉曲面\(S\)には常に同じ量の電荷が入ってきて、さらに入ってきた電荷と同じ量の電荷が閉曲面\(S\)から出ていく。前節の図で例えると\(Q_1=Q_2\)であるような状況だ。したがって、閉曲面\(S\)中の電荷密度\(ρ\)は時間変化しない。
この式を式(4)に代入する。
なぜ連続の式は電荷保存則と呼ばれるのか
連続の式(4)は、「電荷密度\(ρ\)は電流の流入や流出によってのみ時間変化する」ことを表している。このことは式(4)を次のように変形させるとわかりやすい。
上の式の右辺が0のときは、閉曲面の外部と内部で全く電荷の行き来がない場合か、定常電流が流れているため閉曲面内の電荷量が変化しない場合かのどちらかである。つまり、「閉曲面全体において電荷の出入りがあったときのみ、閉曲面内での電荷密度が変化する」のである。このことは、電荷は突然閉曲面内で発生したり消滅したりしないことを意味する。
以上をまとめると、今回の連続の式は、閉曲面内において電荷量が保存されることを表しているから、電荷保存則とも呼ばれる。
まとめ
・電流の定義を確認した。
・電荷密度という概念を導入して、定常電流時に満たす式を求めた。
参考文献
・伊東敏雄(2008)『電磁気学 (朝倉物理学選書)』,朝倉書店.
・砂川重信(1987)『電磁気学 (物理テキストシリーズ 4)』,岩波書店.
・砂川重信(1988)『電磁気学―初めて学ぶ人のために』,培風館.

