[mathjax]
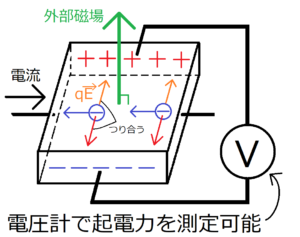
ホール効果とは、磁場中で導体板に電流を流したときに、その導体板に起電力が発生する現象のことである。
この記事では、ホール効果が起こる理由とホール係数について書く。
目次
なぜホール効果が起こるのか
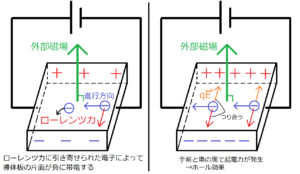
磁場中の導体板に電流を流すと、電流を構成する電子がローレンツ力によって導体板の一面に集まる。すると、電子が集まった面は負に帯電する。そして、逆側の面は相対的に正に帯電する。
時間がたつにつれて電子が負に帯電する面に集まっていくため、この面がつくる電場は徐々に大きくなっていく。これによって、電子がその電場によって受ける力が大きくなっていく。電子が電場から受ける力\(\vec{F}\)は、電子の電荷を\(-e\)、電場を\(\vec{E}\)とすると、次のように表せた。
そして十分時間がたつと、電場による力と磁場によるローレンツ力がつり合うようになる。この2つの力が常に逆向きになるのは、上の図とフレミング左手の法則より明らかである。2つの力がつり合った後からは、電子はローレンツ力の方向に引っ張られることはなくなるため、導体板中の電場はこれ以上増加しない。したがって、一度この2つの力が釣り合ってしまえば、外部磁場が変動したりしない限りはこの状態が維持される。
正に帯電した面と負に帯電した面の電荷は異なるため、当然それぞれの面における電位も異なる。だから、一番上の図のようにそれぞれの面をつないだときに、電位差を観測できるのだ。この電位差はホール効果によって生み出されたものだから、この起電力のことをホール起電力とよぶ。
ホール起電力の求め方
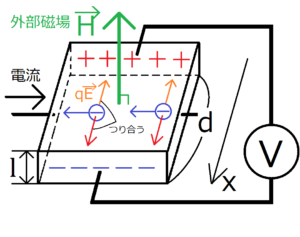
電子に加わる磁場による力と電場による力のつり合いを利用する。
磁場による力の大きさ
外部磁場の磁束密度の大きさを\(B\)、電子の速度を\(v\)、電子の電荷を\(-e\)とする。このとき電子にかかる力の大きさ\(F_B\)は次のようになる。
電子の進行方向(図中の青い矢印)と磁束密度の間の角度は90°だから、sin90°となる。
電場による力の大きさ
前述したが、電子にかかる力の大きさ\(F_E\)は、電場の大きさ\(E\)を使うと次のようになる。
つり合いの式
この2つの力が電子に逆向きにかかっていて、つりあっている。つまり、これらの力がかかっている方向には電子は動かない。よって、上の運動方程式の右辺は0になる。
これを電場\(E\)について解く。
起電力の求め方
電場を位置で積分するとホール起電力\(V_H\)が求まる。
参考:電位とは
ホール係数とは
単位体積中の電荷の個数を\(n\)、電荷の速度を\(v\)、粒子の電荷を\(e\)とすると、電流密度\(J\)について次の関係式が成り立つ。
これを\(v\)について解いて、起電力の式に代入する。
ここで、ホール係数\(R_H\)を
と定義すると、次の関係式を得る。
ホール起電力\(V_H\)、外部磁場\(B\)、磁場方向の試料の長さ\(d\)は測定可能である。電流密度も、試料を流れる電流と試料の断面積が測定できれば求められる。
したがって、ホール係数\(R_H\)は測定によって求められる。
ホール係数の用途
上で定義したように、ホール係数\(R_H\)は電荷\(e\)を含む。このことは、このホール係数の正負を見ることで、試料のキャリアの種類を調べられることを意味する。
キャリアとは、電荷の移動に使われる粒子のことである。キャリアには2種類あり、1つは正の電荷をもつホール(正孔)で、もう1つは負の電荷をもつ自由電子である。ホールは厳密には粒子ではないが、周囲が電子で満たされているため相対的に正に帯電している粒子とみなせる。電子で埋まった場所に空いた穴だからホールというのである。
このホールをキャリアとして使う半導体をp型半導体、一方自由電子をキャリアとして使う半導体をn型半導体という。
p型半導体とn型半導体をくっつけたものをpn接合という。このpn接合は、ダイオードに使われる。
まとめ
・ホール効果とは、外部磁場中の導体に電流を流すと、その導体自身が起電力をつくることである。
・ホール係数の符号を調べることで、半導体の種類を確認できる。
参考文献
・平井紀光(2000)『〔入門〕電気磁気学』,ムイスリ出版.

