分配関数とカノニカル分布の導出

重要なお知らせあなたのWebブラウザーでJavaScriptを有効にする方法

[mathjax]

分配関数 $Z$ を定義することで、系のヘルムホルツの自由エネルギー $F$ と内部エネルギー $E$ が簡単に求まる。

この記事では、その前段階として、カノニカル分布(正準分布)と分配関数 $Z$ を導出する。

目次 [hide]

1 状態の数の復習
系Aが状態 $σ$ をとる確率 $p_σ$
- 2.1 今回考える系Aの仮定と求めたい確率
- 2.2 系Aと熱浴が特定の値のエネルギーを持つ確率
確率 $p_σ$ の変形
- $p_σ$ の規格化
分配関数 $Z$ の定義
5 まとめ
6 参考文献

状態の数の復習

高校で学んだ通りだが、状態の数とは、とある事象が起こりうるすべての組み合わせの総数のことである。例えば、それぞれの面に1から6までの数字が書いてある6面サイコロを一回投げたときに、偶数が出る事象の場合の数は、当然 $W’=3$ となる。

さらに、その6面サイコロがとりうるすべての状態の数は $W=6$ である。そのため、一回投げた時に偶数が出る確率 $p$ はそれらの比で表されるから、 $p$ は次のようになる。

$p=\frac{W’}{W}=\frac{3}{6}=\frac{1}{2}$

このことをもっと一般的な表現にしてみよう。要するに確率 $p$ とは、

$p=\frac{(とある事象が起こる状態の数)}{(系がとりうるすべての状態の数)}$

で表されるのだ。

系Aが状態 $σ$ をとる確率 $p_σ$

今回考える系Aの仮定と求めたい確率

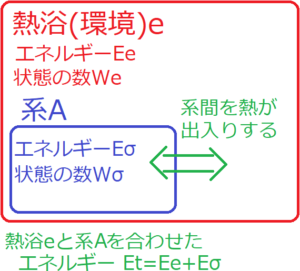
今、熱浴の中にある系Aについて考える。この系Aと熱浴(熱源)の間で、熱は出入りできるが、粒子は出入りできない。また、2つの系全体でみると、熱と粒子のどちらも出入りできない孤立系であるとする。さらに、熱浴のエネルギー $E_e$ のほうが系Aのエネルギー $E_A$ よりもはるかに大きい( $E_e>>E_A$ )。

この系Aのエネルギー $E_A$ が $E_σ$ となる状態を $σ$ とする。以上の仮定をもとに、系Aが状態 $σ$ をとる確率 $p_σ$ を求めよう。

系Aと熱浴が特定の値のエネルギーを持つ確率

2つの系全体で孤立系となることから、これらの系全体のエネルギー $E_t$ は常に熱浴のエネルギー $E_e$ と系Aのエネルギー $E_σ$ の和となることと、 $E_t$ が一定であることがわかる。

$E_t=E_e+E_σ･･･(1)$

この式から、系Aのエネルギーが $E_σ$ になることと、熱浴のエネルギーが $E_t-E_σ$ になることは同値であることがわかる。したがって、系Aのエネルギーが $E_σ$ となる確率 $p_σ$ と、熱浴のエネルギーが $E_t-E_σ$ となる確率は等しくなる。

$\begin{eqnarray}p_σ&=&p_A(E_σ)\\&=&p_{熱浴}(E_e)\\&=&p_{熱浴}(E_t-E_σ)\end{eqnarray}$

ここで、熱浴がとりうるすべての状態の数は、明らかに状態 $σ$ に依存しないため、 $p_σ$ は $W_e(E_t-E_σ)$ に比例する。

$p_σ∝W_e(E_t-E_σ)･･･(2)$

ここからは、この式の右辺について詳しく考えていく。この右辺を求めて、あとは $\sum_σ p_σ=1$ を満たすように規格化すれば、 $p_σ$ が求められそうだ。

確率 $p_σ$ の変形

式(2)の両辺の自然対数をとってみる。

$lnp_σ∝lnW_e(E_t-E_σ)･･･(3)$

$lnW_e(E_t-E_σ)$ を、 $E_σ=0$ についてマクローリン展開する。

$\begin{eqnarray} lnW_e(E_t-E_σ)&=&lnW_e(E_t)+\left.\frac{d(lnW_e(E_t-E_σ))}{dE_σ}\right|_{E_σ=0}･E_σ\\&& \ +\left.\frac{1}{2!}\frac{d^2}{dE_σ^2}(lnW_e(E_t-E_σ))\right|_{E_σ=0}･E_σ^2+･･･\\&≒&lnW_e(E_t)+\left.\frac{d(lnW_e(E_t-E_σ))}{d(E_t-E_σ)}\right|_{E_σ=0}\left.\frac{d(E_t-E_σ)}{dE_σ}\right|_{E_σ=0}･E_σ\\&=&lnW_e(E_t)-\frac{d}{dE_e}(lnW_e(E_e))･E_σ \end{eqnarray}$

もし、総内部エネルギー $E_t$ が、系Aの内部エネルギー $E_σ$ よりも十分に大きい( $E_t>>E_σ$ )ならば、上のように展開の2乗項以降は無視できる。このように近似して、式(3)に代入する。

$\begin{eqnarray} lnp_σ&∝&lnW_e(E_t-E_σ)\\&≒&lnW_e(E_t)-\frac{d}{dE_e}(lnW_e(E_e))･E_σ\\&=&lnW_e(E_t)-\frac{1}{k_B}\frac{dS_e}{dE_e}･E_σ\\&=&lnW_e(E_t)-\frac{1}{k_BT}E_σ･･･(4) \end{eqnarray}$

上の変形の途中で、ボルツマンの関係式

$S_e=k_BlnW_e$

と、エントロピーについての関係式

$\frac{dS}{dE}=\frac{1}{T}$

を使った。

参考:ボルツマンの関係式の導出

参考:エントロピーの定義とは

この式(4)を、次のように変形させる。

$e^{(右辺)}=e^{lnp_σ}=p_σ$

$e^{(左辺)}=W_e(E_t)e^{-\frac{1}{k_BT}E_σ}$

以上より、

$p_σ=Ce^{-\frac{1}{k_BT}E_σ}･･･(5)$

が求まる。ただし、 $W_e(E_t)$ は $E_σ$ に依存しないため、比例定数 $C$ に含めた。

$p_σ$ の規格化

後は式(5)を、 $\sum_σ p_σ=1$ を満たすように規格化すればよい。

$\begin{eqnarray}\sum_σ p_σ&=&C\sum_σ e^{-\frac{1}{k_BT}E_σ}\\&=&1\end{eqnarray}$

この式から定数 $C$ が求められる。そして最終的な $p_σ$ は次のようになる。

$p_σ=\frac{1}{\displaystyle \sum_{σ} e^{-\frac{1}{k_BT}E_{σ}}}e^{-\frac{1}{k_BT}E_σ}･･･(6)$

このように、系Aが状態 $σ$ をとる確率 $p_σ$ を表した確率分布のことを、カノニカル分布(正準分布)とよぶ。

分配関数 $Z$ の定義

式(6)の分母が分配関数と呼ばれるものである。

$\displaystyle Z≡\sum_{σ} e^{-\frac{1}{k_BT}E_{σ}}$

分配関数 $Z$ を使うと、式(6)は次のように書き直せる。

$p_σ=\frac{1}{Z}e^{-\frac{1}{k_BT}E_σ}･･･(7)$

この式(7)中の $\frac{1}{k_BT}$ は、よく $β$ と置き換えられる。

$β≡\frac{1}{k_BT}$

この $β$ を逆温度とよぶ。これを使って式(7)を書き換える。

$p_σ=\frac{1}{Z}e^{-βE_σ}$

まとめ

・カノニカル分布と分配関数を導出した。

参考文献

・小田垣孝(2003)『統計力学』,裳華房.

・藤井勝彦(1990)『統計力学』,マグロウヒル出版株式会社.

・村上雅人(2017)『なるほど統計力学』,海鳴社.

分配関数とカノニカル分布の導出

状態の数の復習