1. /
  2. /
  3. 分配関数を用いた2準位系のエネルギーの考察

分配関数を用いた2準位系のエネルギーの考察

  • このエントリーをはてなブックマークに追加
  • LINEで送る

[mathjax]

分配関数を使えば、2準位系の集合体の内部エネルギー\(E\)とヘルムホルツの自由エネルギー\(F\)を求めることができる。

2準位系の例として、平行磁場中の粒子のスピン(自転)が挙げられる。この記事では、この磁場中の粒子の集合体のエネルギーを、分配関数を使って求める。

分配関数の復習

$$\displaystyle Z≡\sum_{σ} e^{-βE_{σ}}$$
$$p_σ=\frac{1}{Z}e^{-βE_σ}$$

参考:分配関数とカノニカル分布の導出

$$E=k_BT^2\frac{∂}{∂T}lnZ$$
$$F=-\frac{∂}{∂β}lnZ$$

参考:カノニカル分布による自由エネルギーの導出

エネルギー導出の流れ

分配関数からどうすれば内部エネルギーとヘルムホルツの自由エネルギーが求まるのか、その流れを示す。

1.今回考える系の設定をする

2.分配関数を求める

3.それぞれのエネルギーと分配関数の関係式から、\(E\)と\(F\)を求める

今回考える系の設定

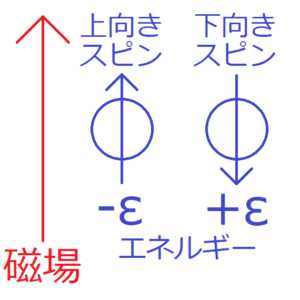
粒子のスピンの向きは、外部磁場に平行または反平行のどちらとする。そして、粒子が持つエネルギーは、スピンが磁場に平行である場合と反平行である場合でそれぞれ\(-ε\)と\(+ε\)である。このような粒子が\(N\)個集合した系を考える。

分配関数の求め方

とある系の状態\(σ\)でのエネルギー\(E_σ\)

\(i\)番目の粒子のエネルギーを\(E_i\)とする。

とある系の状態\(σ\)での\(N\)個の粒子の総エネルギー\(E_σ\)は

$$\displaystyle E_σ=\sum_{i=1}^N E_i$$

であるから、これを後で分配関数の\(E_σ\)に組み込む。

系がとりうるすべての状態と分配関数

さらに、分配関数\(Z\)の定義式中のシグマ\(\sum\)は、「系がとりうるすべての状態を足し合わせる」という意味であった。今回の系では、数式は次のようになる。

\begin{eqnarray}\displaystyle Z&=&\sum_σ e^{-βE_i}\\&=&\sum_{E_1=\pm ε}\sum_{E_2=\pm ε}･･･\sum_{E_N=\pm ε} e^{-β\sum_{i=1}^N E_i}\\&=&\sum_{E_1=\pm ε}\sum_{E_2=\pm ε}･･･\sum_{E_N=\pm ε} e^{-β(E_1+E_2+･･･+E_N)}\\&=&\sum_{E_1=\pm ε}e^{-βE_1}\sum_{E_2=\pm ε}e^{-βE_2}･･･\sum_{E_N=\pm ε} e^{-βE_N}\\&=&(e^{βε}+e^{-βε})･(e^{βε}+e^{-βε})･･･(e^{βε}+e^{-βε})\\&=&(e^{βε}+e^{-βε})^N\end{eqnarray}

ヘルムホルツの自由エネルギーと内部エネルギー

まずヘルムホルツの自由エネルギー\(F\)を求める。

\begin{eqnarray}F&=&-k_BTlnZ\\&=&-k_BTln(e^{βε}+e^{-βε})^N\\&=&-k_BTNln(e^{βε}+e^{-βε})\end{eqnarray}

次に内部エネルギー\(E\)を求める。

\begin{eqnarray}E&=&-\frac{∂}{∂β}lnZ\\&=&-\frac{∂}{∂β}ln(e^{βε}+e^{-βε})^N\\&=&-N\frac{∂}{∂β}ln(e^{βε}+e^{-βε})\\&=&-N\frac{∂}{∂β}ln(e^{βε}+e^{-βε})\\&=&-Nε\frac{e^{βε}-e^{-βε}}{e^{βε}+e^{-βε}}\\&=&-Nεtanh(βε)\end{eqnarray}

\(E\)をグラフ化する。

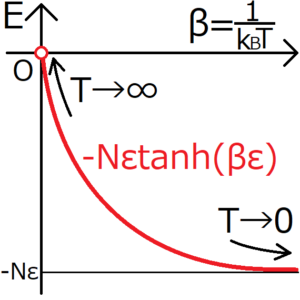
このグラフから、次の２つのことがいえる。

・総エネルギー\(E\)が\(0\)という状況は、上向きスピンの粒子と下向きスピンの粒子の数が全く同じことを表している。つまり、\(T \to ∞\)という極限では、粒子のスピンの向きはランダムになると考えられる。

・総エネルギー\(E\)が\(-Nε\)という状況は、すべての粒子のスピンが磁場と同じ向きを向いていることを表している。つまり、絶対温度\(T\)が絶対零度付近では、粒子のスピンのほとんどが、磁場と同じ向きを向いているといえる。絶対零度付近ではエネルギーが最小になるようなスピンになるとも言い換えができるだろう。

まとめ

・磁場中の粒子のスピンを例に、2準位系の集合体の分配関数と、そのエネルギーについて考察した。

参考文献

・小田垣孝(2003)『統計力学』,裳華房.

・藤井勝彦(1990)『統計力学』,マグロウヒル出版株式会社.

・村上雅人(2017)『なるほど統計力学』,海鳴社.

  • このエントリーをはてなブックマークに追加
  • LINEで送る

SNSでもご購読できます。

コメントを残す

*

CAPTCHA