ポテンシャル障壁によるトンネル効果の計算

重要なお知らせあなたのWebブラウザーでJavaScriptを有効にする方法

[mathjax]

前の記事で、シュレディンガー方程式を使って波動関数を求めるということは、粒子の位置を示す確率密度を求めることであると結論付けた。

この記事では、一次元矩形型ポテンシャルを例に、実際にシュレディンガー方程式を解く。さらに、反射率と透過率も求める。

参考:シュレディンガー方程式を解く意味とは

参考:確率流密度と連続の式の導出

シュレディンガー方程式の確認

一次元のシュレディンガー方程式は次で与えられる。ここで、 $E$ は粒子のエネルギー固有地である。

$\left( -\frac{ħ^2}{2m}\frac{∂^2}{∂x^2} +V(x) \right) ψ(x)=Eψ(x)$

参考:シュレディンガー方程式と運動量演算子の求め方

そして、波動関数の絶対値の2乗が、粒子の確率密度を表している。

$ρ=|ψ(x,t)|^2$

参考:シュレディンガー方程式を解く意味とは

参考:確率流密度と連続の式の導出

今回考える矩形波ポテンシャル

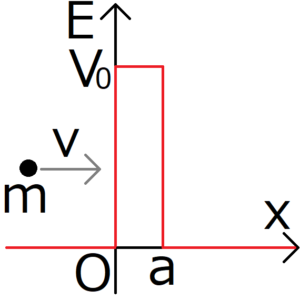
上の図のような矩形波ポテンシャルを考える。数式で表すと次のようになる。

$\begin{eqnarray} V(x)=\begin{cases} V_0 & (0<x<a) \\ 0 & (x<0, \ a<x) \end{cases}\end{eqnarray}$

今回は、このポテンシャルの左側( $x \to -∞$ )から、質量 $m$ の粒子を飛ばした場合を考える。

さらに、エネルギー固有値 $E$ がポテンシャル障壁 $V_0$ 未満であるとも仮定する。

$0<E<V_0$

この場合、古典的に考えれば、粒子は障壁を超えることは不可能である。ところが、もし量子力学的に考えたら･･･?

トンネル効果とは何か

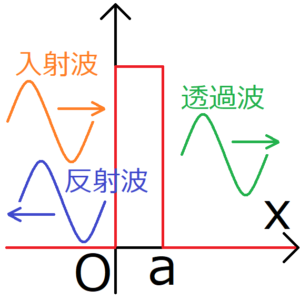
粒子を波として考えると、粒子を飛ばすという動作は、波を入射させる動作に置き換えることができる。するとその入射波は、ポテンシャルで反射される反射波と、ポテンシャルを通り抜ける透過波に分けられると考えられる。

透過波が存在するということは、ポテンシャルを通り抜けた先にも存在確率が発生することを意味する。したがって、左側から飛ばした粒子が、ポテンシャルを超えた向こう側にも存在する可能性が生じる。

もしポテンシャルの奥で粒子が観測されたら、その粒子は本来超えられるはずがないポテンシャルを通り抜けたことになる。これがトンネル効果である。

では、これからシュレディンガー方程式を使って、実際に反射率と透過率を求めてみよう。

シュレディンガー方程式の解き方

実際にシュレディンガー方程式を解いてみる。

ポテンシャルの分割

上の矩形波ポテンシャルは、ポテンシャルの手前、ポテンシャル中、ポテンシャルの奥の3つの領域に分けることができる。

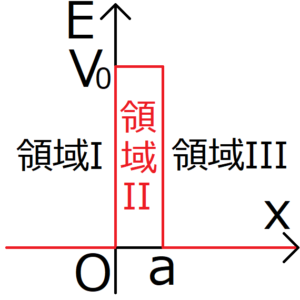
それぞれの領域でポテンシャルと境界条件が異なるため、領域ごとにシュレディンガーを組み立てなければならない。

領域Iと領域IIIではポテンシャルが両方とも0のため、一見同じ波動関数が得られるように見えるかもしれない。ところが、領域Iは $x \to -∞$ で、領域IIIは $x \to +∞$ でそれぞれ波動関数が発散しないようにする必要がある。そのため、やはり別物と考えたほうがよい。

領域Iの波動関数

この領域のポテンシャルは0であるため、解くべきシュレディンガー方程式は次のようになる。

$-\frac{ħ^2}{2m}\frac{∂^2}{∂x^2} ψ_{I}(x,t)=Eψ_{I}(x)$

これは単純な微分方程式である。 $-\frac{ħ^2}{2m}$ を右辺に押し付けたほうがわかりやすいか。

$\frac{∂^2}{∂x^2} ψ_{I}(x)=-\frac{2mE}{ħ^2}ψ_{I}(x)$

以降、右辺の $\frac{2mE}{ħ^2}$ を $k^2$ とおく。

$\frac{∂^2}{∂x^2} ψ_{I}(x,t)=-k^2ψ_{I}(x,t)$

この微分方程式の解は、定数 $C_1,C_2$ を用いると、 $C_1e^{ikx}$ と $C_2e^{-ikx}$ の線形結合となる。不安ならば代入してみよう。

$ψ_{I}(x)=C_1e^{ikx}+C_2e^{-ikx}$

$C_1e^{ikx}$ は右側に進む波、つまり入射波を表す。一方 $C_2e^{-ikx}$ は左側に進む波、つまり反射波を表す。

領域IIの波動関数

同様にして、領域IIの波動関数も求める。

$\left( -\frac{ħ^2}{2m}\frac{∂^2}{∂x^2} +V_0 \right) ψ_{II}(x)=Eψ_{II}(x)$

この方程式も、次のように整理すれば見通しがつきやすい。 $E<V_0$ に注意する。

$\frac{∂^2}{∂x^2}ψ_{II}(x)=\frac{2m(V_0-E)}{ħ^2}ψ_{II}(x)$

ここで、 $κ^2≡\frac{2m(V_0-E)}{ħ^2}$ とおくと、波動関数は次のように求まる。

$ψ_{II}(x)=C’_1e^{κx}+C’_2e^{-κx}$

領域IIIの波動関数

ポテンシャルが0のため、境界条件を求める直前までは同じである。

$ψ_{III}(x)=C”_1e^{ikx}+C”_2e^{-ikx}$

ただし、今回は障壁の左側からのみ粒子を飛ばすため、右側( $x \to +∞$ )からくる粒子はない。したがって、この領域IIIで左向きに進む波は存在しない。

$C”_2e^{-ikx}=0$

したがって、 $ψ_{III}(x)$ は次のようになる。

$ψ_{III}(x)=C”_1e^{ikx}$

波動関数の境界条件

前述したように、それぞれの波動関数は境界において滑らかに接続されなければならない。「滑らかに接続」とは、境界における値とその一階微分が等しくなることである。

今回の場合、 $x=0$ における領域Iと領域IIの波動関数と、 $x=a$ における領域IIと領域IIIの波動関数がそれぞれ滑らかに接続される必要がある。つまり、数式で表すと次のようになる。

$\begin{eqnarray} \begin{cases} &ψ_{I}(0)=ψ_{II}(0) \\ &\left.\frac{dψ_{I}(0)}{dx}\right|_{x=0}=\left.\frac{dψ_{II}(x)}{dx}\right|_{x=0} \end{cases}\end{eqnarray}$

$\begin{eqnarray} \begin{cases} &ψ_{II}(a)=ψ_{III}(a) \\ &\left.\frac{dψ_{II}(x)}{dx}\right|_{x=a}=\left.\frac{dψ_{III}(x)}{dx}\right|_{x=a} \end{cases}\end{eqnarray}$

それぞれの場合を考えていく。

領域Iと領域IIの境界(x=0)

$ψ_{I}(0)=ψ_{II}(0)$

だから、

$C_1e^{ik0}+C_2e^{-ik0}=C’_1e^{κ0}+C’_2e^{-κ0}.$

$e^0=1$ であったから、

$C_1+C_2=C’_1+C’_2･･･(1)$

となる。さらに

$\left.\frac{dψ_{I}(0)}{dx}\right|_{x=0}=\left.\frac{dψ_{II}(x)}{dx}\right|_{x=0}$

だから、

$ik(C_1-C_2)=κ(C’_1-C’_2)･･･(2)$

となる。

領域IIと領域IIIの境界(x=a)

$ψ_{II}(a)=ψ_{III}(a)$

だから、

$C’_1e^{κa}+C’_2e^{-κa}=C”_1e^{ika}･･･(3)$

となる。さらに

$\left.\frac{dψ_{II}(x)}{dx}\right|_{x=a}=\left.\frac{dψ_{III}(x)}{dx}\right|_{x=a}$

だから、

$κ(C’_1e^{κa}-C’_2e^{-κa})=ikC”_1e^{ika}･･･(4)$

となる。

連立方程式を解く

式(1)から式(4)までの方程式を、 $C_1$ , $C_2$ , $C’_1$ , $C’_2$ , $C”_1$ を変数とした連立方程式として解く。ところが、変数5つに対して方程式は4つしかないため、それぞれの変数の正確な値は求まらない。

ただし、それでも変数の比までは求めることができる。今回の最終目標は透過率と反射率を求めることだから、それらの比さえ求まれば十分である。

後述するが、確率密度の反射率 $R$ と透過率 $T$ は次のように定義される。

$R=\frac{|C_2|^2}{|C_1|^2}$

$T=\frac{|C”_1|^2}{|C_1|^2}$

一見 $C_1$ と $C_2$ の両方が含まれる式(1)と式(2)だけで反射率 $R$ が求められそうだが、これらの式には他にも関係ない変数が2つ( $C’_1$ と $C’_2$ )も含まれているため、この2式だけでは反射率を求めることはできない。

では、 $C’_1$ と $C’_2$ をそれぞれ他の共通な1種類の変数を含む形に変形できたらどうだろうか。そうすれば、その変形させた $C’_1$ と $C’_2$ を式(1)と式(2)に代入することで、反射率が求められそうだ。

実はこの変形は、式(3)と式(4)を使えば可能である。これからその変形をしてみる。

$C’_1$ と $C’_2$ の変形

係数 $C’_1$ と $C’_2$ を、共通な変数 $C”_1$ を使った形に変形させる。

$C’_1e^{κa}+C’_2e^{-κa}=C”_1e^{ika}･･･(3)$

$κ(C’_1e^{κa}-C’_2e^{-κa})=ikC”_1e^{ika}･･･(4)$

式(4)の両辺を $κ$ で割って、式(3)と式(4)を足せば $C’_1$ 、引けば $C’_2$ が求められそうだ。

$\begin{eqnarray} C’_1&=&C”_1\frac{e^{ika}}{2e^{κa}} \left( 1+\frac{ik}{κ} \right) \\&=&\left( \frac{(κ+ik)e^{ika}}{2κe^{κa}} \right)C”_1\end{eqnarray}$

$\begin{eqnarray} C’_2&=&C”_1\frac{e^{ika}}{2e^{-κa}} \left( 1-\frac{ik}{κ} \right) \\&=&\left( \frac{(κ-ik)e^{ika}}{2κe^{-κa}} \right)C”_1\end{eqnarray}$

$C_1$ と $C_2$ の変形

上で変形させた $C’_1$ と $C’_2$ を、式(1)と式(2)に代入させる。

$\begin{eqnarray}C_1+C_2&=&C”_1\left( \frac{(κ+ik)e^{ika}}{2κe^{κa}} + \frac{(κ-ik)e^{ika}}{2κe^{-κa}} \right)\\&=&\frac{C”_1e^{ika}}{2κ}\left[ (κ+ik)e^{-κa} + (κ-ik)e^{κa} \right]\\&=&\frac{C”_1e^{ika}}{2ikκ}\left[ (ikκ-k^2)e^{-κa} + (ikκ+k^2)e^{κa} \right]\end{eqnarray}$

$\begin{eqnarray}C_1-C_2&=&\frac{κ}{ik}C”_1\left( \frac{(κ+ik)e^{ika}}{2κe^{κa}} – \frac{(κ-ik)e^{ika}}{2κe^{-κa}} \right)\\&=&\frac{C”_1e^{ika}}{2ikκ}\left[ (κ^2+ikκ)e^{-κa} – (κ^2-ikκ)e^{κa} \right] \end{eqnarray}$

この式の両辺をそれぞれ足せば $C_1$ 、引けば $C_2$ が求まる。

$\begin{eqnarray}C_1&=&\frac{1}{2}\frac{C”_1e^{ika}}{2ikκ}\left[ (ikκ-k^2)e^{-κa} + (ikκ+k^2)e^{κa}+[(κ^2+ikκ)e^{-κa} – (κ^2-ikκ)e^{κa}] \right]\\&=&\frac{C”_1e^{ika}}{4ikκ}\left[ (k^2+2ikκ-κ^2)e^{κa} + (κ^2+2ikκ-k^2)e^{-κa} \right]\\&=&\frac{C”_1e^{ika}}{4ikκ}\left[ (k+iκ)^2e^{κa} -(k-iκ)^2e^{-κa} \right]\end{eqnarray}$

$\begin{eqnarray}C_2&=&\frac{1}{2}\frac{C”_1e^{ika}}{2ikκ}\left[ (ikκ-k^2)e^{-κa} + (ikκ+k^2)e^{κa}-[(κ^2+ikκ)e^{-κa} – (κ^2-ikκ)e^{κa}] \right]\\&=&\frac{C”_1e^{ika}}{4ikκ}\left[ (k^2+κ^2)e^{κa} – (k^2+κ^2)e^{-κa} \right]\\&=&\frac{C”_1e^{ika}}{4ikκ}(k^2+κ^2)\left( e^{κa}-e^{-κa} \right)\end{eqnarray}$

反射率と透過率の導出

元の波動関数を見直すと、 $C_1$ は入射波、 $C_2$ は反射波、 $C”_1$ は透過波の振幅であることを確認できる。したがって、これらを使って確率密度の反射率 $R$ と透過率 $T$ を示すと次のようになる。

$R≡\frac{|C_2|^2}{|C_1|^2}$

$T≡\frac{|C”_1|^2}{|C_1|^2}$

これらに上で求めた定数を代入すれば、 $C_1$ と $C_2$ のそれぞれに含まれる $C”_1$ がキャンセルされて、変数を含まない反射率と透過率が求まる。

最終結果を見やすくするため、双曲線関数

$sinh(ax)=\frac{e^{ax}-e^{-ax}}{2}$

$cosh(ax)=\frac{e^{ax}+e^{-ax}}{2}$

を導入すると、反射率と透過率はそれぞれ次のように計算される。

$\begin{eqnarray}R&=&\left|\frac{C_2}{C_1}\right|^2\\&=&\left|\frac{(k^2+κ^2)( e^{κa}-e^{-κa})}{(k+iκ)^2e^{κa} -(k-iκ)^2e^{-κa}}\right|^2\\&=&\left|\frac{(k^2+κ^2)( e^{κa}-e^{-κa})}{(k^2-κ^2)e^{κa} -(k^2-κ^2)e^{-κa}+2ikκ(e^{κa}+e^{-κa})}\right|^2\\&=&\left|\frac{(k^2+κ^2)( e^{κa}-e^{-κa})}{(k^2-κ^2)(e^{κa}-e^{-κa}) +2ikκ(e^{κa}+e^{-κa})}\right|^2\\&=&\left|\frac{2(k^2+κ^2)sinh(κa)}{2(k^2-κ^2)sinh(κa) +4ikκcosh(κa)}\right|^2\\&=&\left|\frac{(k^2+κ^2)sinh(κa)}{(k^2-κ^2)sinh(κa) +2ikκcosh(κa)}\right|^2\\&=&\left|\frac{(k^2+κ^2)sinh(κa)}{[(k^2-κ^2)sinh(κa) +2ikκcosh(κa)][(k^2-κ^2)sinh(κa) -2ikκcosh(κa)]}[(k^2-κ^2)sinh(κa) -2ikκcosh(κa)]\right|^2\\&=&\left|\frac{(k^2+κ^2)sinh(κa)}{[(k^2-κ^2)sinh(κa) +2ikκcosh(κa)][(k^2-κ^2)sinh(κa) -2ikκcosh(κa)]}\right|^2\left|[(k^2-κ^2)sinh(κa) -2ikκcosh(κa)]\right|^2\\&=&\frac{(k^2+κ^2)^2sinh^2(κa)}{[(k^2-κ^2)^2sinh^2(κa) +4k^2κ^2cosh^2(κa)]^2}[(k^2-κ^2)^2sinh^2(κa) +4k^2κ^2cosh^2(κa)]\\&=&\frac{(k^2+κ^2)^2sinh^2(κa)}{(k^2-κ^2)^2sinh^2(κa) +4k^2κ^2cosh^2(κa)}\\&=&\frac{(k^2+κ^2)^2sinh^2(κa)}{(k^4-2k^2κ^2+κ^4)sinh^2(κa) +4k^2κ^2cosh^2(κa)}\\&=&\frac{(k^2+κ^2)^2sinh^2(κa)}{(k^4+2k^2κ^2+κ^4)sinh^2(κa)-4k^2κ^2sinh^2(κa) +4k^2κ^2cosh^2(κa)}\\&=&\frac{(k^2+κ^2)^2sinh^2(κa)}{(k^2+κ^2)^2sinh^2(κa)+4k^2κ^2(cosh^2(κa)-sinh^2(κa))}\\&=&\frac{(k^2+κ^2)^2sinh^2(κa)}{(k^2+κ^2)^2sinh^2(κa)+4k^2κ^2}\end{eqnarray}$

$\begin{eqnarray}T&=&\left|\frac{C”_1}{C_1}\right|^2\\&=&\left|C”_1･\frac{4ikκ}{C”_1e^{ika}}\frac{1}{(k+iκ)^2e^{κa} -(k-iκ)^2e^{-κa}}\right|^2\\&=&\left|\frac{4ikκ}{e^{ika}}\frac{1}{2(k^2-κ^2)sinh(κa) +4ikκcosh(κa)}\right|^2\\&=&\left|e^{-ika}\frac{2ikκ}{(k^2-κ^2)sinh(κa) +2ikκcosh(κa)}\right|^2\\&=&\left|e^{-ika}\frac{2ikκ[(k^2-κ^2)sinh(κa)-2ikκcosh(κa)]}{[(k^2-κ^2)sinh(κa) +2ikκcosh(κa)][(k^2-κ^2)sinh(κa)-2ikκcosh(κa)]}\right|^2\\&=&\left|e^{-ika}\frac{2ikκ}{(k^2-κ^2)^2sinh^2(κa) +4k^2κ^2cosh^2(κa)}[(k^2-κ^2)sinh(κa)-2ikκcosh(κa)]\right|^2\\&=&\left|e^{-ika}\right|^2\left|\frac{2ikκ}{(k^2-κ^2)^2sinh^2(κa) +4k^2κ^2cosh^2(κa)}\right|^2\left|(k^2-κ^2)sinh(κa)-2ikκcosh(κa)\right|^2\\&=&1^2･\left|\frac{-4k^2κ^2}{[(k^2-κ^2)^2sinh^2(κa) +4k^2κ^2cosh^2(κa)]^2}\right|[(k^2-κ^2)^2sinh^2(κa)+4k^2κ^2cosh^2(κa)]\\&=&\frac{4k^2κ^2}{(k^2-κ^2)^2sinh^2(κa) +4k^2κ^2cosh^2(κa)}\\&=&\frac{4k^2κ^2}{(k^2+κ^2)^2sinh^2(κa)+4k^2κ^2}\end{eqnarray}$

以上で、反射率と透過率が求められた。

$R=\frac{(k^2+κ^2)^2sinh^2(κa)}{(k^2+κ^2)^2sinh^2(κa)+4k^2κ^2}$

$T=\frac{4k^2κ^2}{(k^2+κ^2)^2sinh^2(κa)+4k^2κ^2}$

式をなぞっているだけだとかなり複雑な計算に思えるかもしれない。ところが、双曲線関数の公式さえ分かっていれば、あとは実際は分母を有理化したり複素数の絶対値を求めたりしているだけで、見た目ほど難しいことはしていない。

ただし、 $|e^{ika}|^2=1$ には気を付けよう。複素平面上での $e^{ika}$ が半径1の円になっていることを思い出せば、納得できるはずだ。

反射率と透過率の関係

反射率と透過率の和は1になる。

$\begin{eqnarray}R+T&=&\frac{(k^2+κ^2)^2sinh^2(κa)}{(k^2+κ^2)^2sinh^2(κa)+4k^2κ^2}+\frac{4k^2κ^2}{(k^2+κ^2)^2sinh^2(κa)+4k^2κ^2}\\&=&1\end{eqnarray}$

このことは、左側から飛ばした粒子は、ポテンシャルによって反射されるか、ポテンシャルを通り抜けるかのどちらかとなることを意味する。

透過率の近似

双曲線関数 $sinh(κa)$ の定義を見直すと、 $κa$ が十分1より大きいとき、つまり

$a\sqrt{\frac{2m(V_0-E)}{ħ^2}}>>1$

を満たすとき(粒子のエネルギー $E$ がポテンシャル $V_0$ よりも十分小さいとき)、

$sinh(κa)≒\frac{1}{2}e^{κa}$

と近似できることがわかる。これを利用して、透過率 $T$ の形を簡単にできる。

$\begin{eqnarray}T&=&\frac{4k^2κ^2}{(k^2+κ^2)^2sinh^2(κa)+4k^2κ^2}\\&=&\frac{1}{\frac{(k^2+κ^2)^2}{4k^2κ^2}sinh^2(κa)+1}\\&=&\left[\frac{(k^2+κ^2)^2}{4k^2κ^2}sinh^2(κa)+1\right]^{-1}\\&≒&\left[\frac{(k^2+κ^2)^2}{16k^2κ^2}e^{2κa}+1\right]^{-1}\end{eqnarray}$

$κa>>1$ だから、 $e^{κa}$ は $+1$ が無視できるくらい大きい。

$\begin{eqnarray}T&≒&\left[\frac{(k^2+κ^2)^2}{16k^2κ^2}e^{2κa}+1\right]^{-1}\\&≒&\left[\frac{(k^2+κ^2)^2}{16k^2κ^2}e^{2κa}\right]^{-1}\\&=&\frac{16k^2κ^2}{(k^2+κ^2)^2}e^{-2κa}\\&=&\frac{16\left(\frac{2mE}{ħ^2}\right)\left(\frac{2m(V_0-E)}{ħ^2}\right)}{\left(\frac{2mE}{ħ^2}+\frac{2m(V_0-E)}{ħ^2}\right)^2}e^{-2κa}\\&=&\frac{16\left(2mE\right)\left(2m(V_0-E)\right)}{\left(2mV_0\right)^2}exp\left[-2\sqrt{\frac{2m(V_0-E)}{ħ^2}}a\right]\\&=&\frac{16E(V_0-E)}{V_0^2}exp\left[-\frac{2a}{ħ}\sqrt{2m(V_0-E)}\right]\end{eqnarray}$

この式から、透過率のオーダーは $exp$ の部分で決まることがわかる。したがって、最終的な透過率の近似は次のように書ける。

$T≒exp\left[-\frac{2a}{ħ}\sqrt{2m(V_0-E)}\right]$

ディラック定数が

$ħ≒1.05×10^{-34}J･s$

であることを考慮すると、 $κa>>1$ の場合の透過率がいかに小さいかがわかる。

まとめ

・エネルギー固有値 $E$ が $0<E<V_0$ を満たすときの、反射率と透過率を求めた。

・反射率と透過率の和は1になる。

参考文献

・村上雅人(2006)『なるほど量子力学II』,海鳴社.

ポテンシャル障壁によるトンネル効果の計算

シュレディンガー方程式の確認