原点に向かって変位\(x\)に比例する大きさの力\(f\)が物体に働いている。
$$f=-kx$$
このような力による運動を単振動(調和振動)という。さらに単振動をする系を調和振動子という。
目次
単振動する物体の軌跡
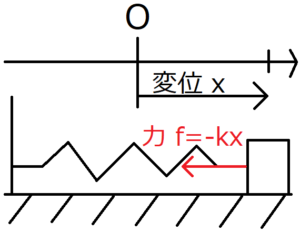
ばねにつながれた質量\(m\)の物体を変位\(x_0(>0)\)の位置まで持っていき、時刻\(t=0\)で手を離した時の物体の軌跡\(x(t)\)を求めよう。ただし、ばねのつり合いの位置を原点とし、摩擦や空気による抵抗はないとする。
運動方程式と軌跡
運動方程式\(f=m\frac{d^2x}{dt^2}\)を上式に代入する。
この微分方程式を解く。まずは両辺を\(m\)で割る。
\(\ddot{x}=-αx\)という形の微分方程式の解は、\(x(t)=Ce^{\pm i\sqrt{α}t}\)という形となる。実際に代入すればこの解が上の方程式を満たしていることを確認できるが、このくらいは暗記していてもいいかもしれない。
\(\sqrt{\frac{k}{m}}\)が表すもの
上式の右辺の\(\sqrt{\frac{k}{m}}\)は何を表しているのだろうか。
力fの次元
質量\(m\)の次元は\(M\)、加速度\(\ddot{x}\)の次元は\(LT^{-2}\)である。すると力\(f\)の次元は\(f=m\ddot{x}\)より、\([f]=MLT^{-2}\)となる。
\(\sqrt{\frac{k}{m}}\)の次元
距離\(x\)の次元は\(L\)、ばねの方程式\(k=-\frac{f}{x}\)より、\(k\)の次元は次のように求まる。
だから、\(\sqrt{\frac{k}{m}}\)の次元は次のように求まる。
\(T^{-1}\)は角速度の次元である。したがって、\(\sqrt{\frac{k}{m}}\)は角速度を表す。
角速度は一般的に\(ω\)で表されるため、以降次のようにおく。
改めて\(x(t)\)を書き直してみる。
$$x(t)=Cexp\left( \pm iωt \right)$$
初期位相と初期条件
初期位相を\(φ\)とすると\(e^φ\)は定数だから、\(C=C_0e^{iφ}\)とすれば、初期位相を含む解は次のように書ける。
オイラーの公式\(e^{ \pm iθ}=cosθ \pm isinθ\)を適用すると、下のようにも書ける。
これを複素平面上で表してみる。
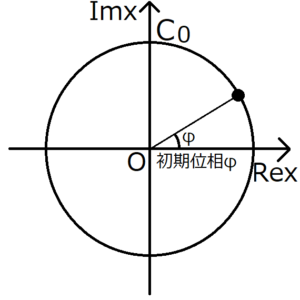
今考えているばねにつながれた物体の動きは、この式の実部を取り出したものである。単振動している物体の運動は円運動を射影したものとよく言われるが、それは複素平面上の円に沿って動いている物体を実部に射影しているからである。
ここで、今考えている系の初期条件を考える。物体は時刻\(t=0\)に\(x_0\)で手を離した瞬間に、原点方向に動く。よって、物体は下の二つの式を得る。
以上をまとめると、位置\(x(t)\)は次の式になる。
cos内の符号
最後に、\(ωt\)にかかっている符号\(\pm\)は、\(cosωt=cos(-ωt)\)だから外すことができる。
一応図でも考えてみる。
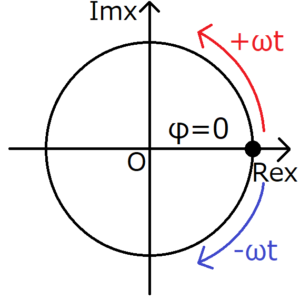
物体が\(+ωt\)の方向で回っても\(-ωt\)の方向で回っても、実軸に射影してしまえば区別がつかなくなる。だから、符号\(\pm\)は取り外せる。
まとめ
・今回はばねのモデルから、単振動する物体の軌跡を求めた。
・単振動の軌跡は次のようにあらわされる。
参考文献
・長谷川修司(2009)『講談社基礎物理学シリーズ2 振動・波動』,講談社.
・戸田盛和(1982)『力学〔物理入門コース1〕』,岩波書店.

