コリオリの力とは

重要なお知らせあなたのWebブラウザーでJavaScriptを有効にする方法

[mathjax]

コリオリの力とは、系$S’$が系$S$に対して回転運動をしているときに発生する見かけ上の力のことである。回転運動で発生する見かけ上の力としては遠心力が有名だが、コリオリの力と遠心力は全くの別物である。

この記事では、コリオリの力は数式でどう表されるのかを示す。

1 静止系と回転系の関係と運動方程式
2 コリオリの力の導出
3 コリオリの力のベクトル表記
- 3.1 結局コリオリの力とはなにか
4 コリオリの力を簡単に実感できる実験
5 まとめ
6 参考文献

静止系と回転系の関係と運動方程式

静止系と回転系

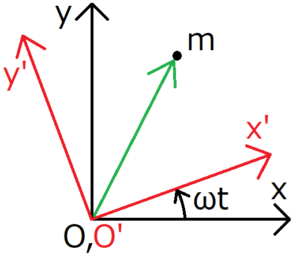
この記事では、黒い線で表されている座標系$S$を静止系、赤い線で表されている座標系$S’$を回転系とする。図からわかるように、両方の系の原点は共通しており、また回転系$S’$は、原点$O’$を軸にして角速度$ω$で回っている。

静止系と回転系の関係

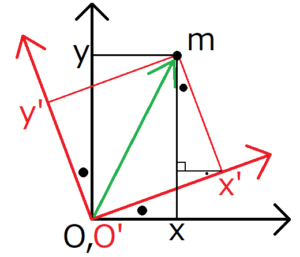
上の図のから、三角形の相似を考えると、黒丸で示した角度はすべて等しいことがわかる。

系$S$からみた力$F_x,F_y$と系$S’$からみた力$F’_x,F’_y$の関係式は、次のようになる。

$$F’_x=F_xcosωt+F_ysinωt･･･(1)$$

$$F’_y=-F_xsinωt+F_ycosωt･･･(2)$$

また、系$S(O-x,y,z)$と系$S'(O’-x’,y’,z’)$の関係は、

$$x=x’cosωt-y’sinωt$$

$$y=x’sinωt+y’cosωt$$

回転系における運動方程式の導出の準備

系$S$の運動方程式に系$S’$の座標を適応するために、両辺を時刻$t$で2階微分する。

\begin{eqnarray}\frac{d^2x}{dt^2}&=&\frac{d^2}{dt^2}(x’cosωt-y’sinωt)\\&=&\frac{d}{dt}\left(\frac{dx’}{dt}cosωt-x’ωsinωt-\frac{dy’}{dt}sinωt-y’ωcosωt\right)\\&=&\left(\frac{d^2x’}{dt^2}cosωt-\frac{dx’}{dt}ωsinωt\right)-\left(\frac{dx’}{dt}ωsinωt+x’ω^2cosωt\right)-\left(\frac{d^2y’}{dt^2}sinωt+\frac{dy’}{dt}ωcosωt\right)-\left(\frac{dy’}{dt}ωcosωt-y’ω^2sinωt\right)\\&=&\frac{d^2x’}{dt^2}cosωt-2\frac{dx’}{dt}ωsinωt-x’ω^2cosωt-\frac{d^2y’}{dt^2}sinωt-2\frac{dy’}{dt}ωcosωt+y’ω^2sinωt\\&=&\left(\frac{d^2x’}{dt^2}-2ω\frac{dy’}{dt}-ω^2x’\right)cosωt-\left(\frac{d^2y’}{dt^2}+2ω\frac{dx’}{dt}-ω^2y’\right)sinωt\end{eqnarray}

\begin{eqnarray}\frac{d^2y}{dt^2}&=&\frac{d}{dt}\left(\frac{dx’}{dt}sinωt+x’ωcosωt+\frac{dy’}{dt}cosωt-y’ωsinωt\right)\\&=&\left(\frac{d^2x’}{dt^2}-2ω\frac{dy’}{dt}-ω^2x’\right)sinωt+\left(\frac{d^2y’}{dt^2}+2ω\frac{dx’}{dt}-ω^2y’\right)cosωt\end{eqnarray}

回転系における運動方程式の導出

$t$の2階微分を系$S$における運動方程式に代入すれば、系$S’$における運動方程式が求まる。

$$m\left(\frac{d^2x’}{dt^2}-2ω\frac{dy’}{dt}-ω^2x’\right)cosωt-m\left(\frac{d^2y’}{dt^2}+2ω\frac{dx’}{dt}-ω^2y’\right)sinωt=F_x･･･(3)$$

$$m\left(\frac{d^2x’}{dt^2}-2ω\frac{dy’}{dt}-ω^2x’\right)sinωt+m\left(\frac{d^2y’}{dt^2}+2ω\frac{dx’}{dt}-ω^2y’\right)cosωt=F_y･･･(4)$$

これらの式の右辺の力$F_x,F_y$は系$S$からみたときの力だから、系$S’$における運動方程式を完成させるためには、これらの力を系$S’$からみたときの力$F’_x,F’_y$に変形させる必要がある。

まず、式(3)の両辺には$cosωt$、式(4)の両辺には$sinωt$をかけて、加工後の式(3)と式(4)の両辺を足すと、次の式を得る。

$$m\left(\frac{d^2x’}{dt^2}-2ω\frac{dy’}{dt}-ω^2x’\right)=F_xcosωt+F_ysinωt$$

ここで、三角関数の関係式$sin^2ωt+cos^2ωt=1$を使った。この式の右辺は、式(1)より、系$S’$からみた力$F’_x$を表す。

同様にして、式(3)の両辺には$sinωt$、式(4)の両辺には$cosωt$をかけて、加工後の式(4)から式(3)の両辺を引くと、次の式を得る。

$$m\left(\frac{d^2y’}{dt^2}+2ω\frac{dx’}{dt}-ω^2y’\right)=-F_xsinωt+F_ycosωt$$

この式の右辺は、式(2)より、系$S’$からみた力$F’_y$を表す。

以上をまとめると、

$$m\left(\frac{d^2x’}{dt^2}-2ω\frac{dy’}{dt}-ω^2x’\right)=F’_x･･･(5)$$

$$m\left(\frac{d^2y’}{dt^2}+2ω\frac{dx’}{dt}-ω^2y’\right)=F’_y･･･(6)$$

コリオリの力の導出

式(5)と式(6)の各項の考察を行う。最初に両方の式の左辺の第二項と第三項を移項して、式(5)と式(6)の運動方程式を$m\ddot{x}=(力)$というおなじみの形にする。

$$m\frac{d^2x’}{dt^2}=F’_x+2mω\frac{dy’}{dt}+mω^2x’･･･(7)$$

$$m\frac{d^2y’}{dt^2}=F’_y-2mω\frac{dx’}{dt}+mω^2y’･･･(8)$$

両式の右辺の第二項がコリオリの力である。質点に実際に働いている力は$F’_x,F’_y$であるため、コリオリの力は見かけ上の力である。実際に質点に作用しているわけではない。

コリオリの力を$F_{Cx},{F_Cy}$とおき、数式で表すと、

$$F_{Cx}=2mω\frac{dy’}{dt}･･･(9)$$

$$F_{Cy}=-2mω\frac{dx’}{dt}･･･(10)$$

ちなみに、式(7)と式(8)の右辺の第三項は遠心力を表している。

参考:遠心力・向心力とは-円運動から学ぶ見かけ上の力

コリオリの力のベクトル表記

式(9)と式(10)より、コリオリの力をベクトルで表すには、質量$m$と角速度ベクトル${\bf ω}$、速度ベクトル${\bf v}$、そしてコリオリの力の向きが分かればよいことになる。

結局コリオリの力とはなにか

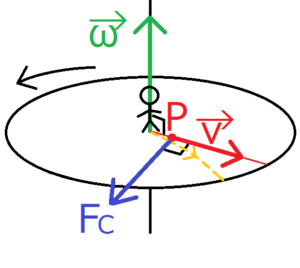
今回はごく簡単な場合について考える。上の図では、左回りで回転する円盤上の観察者(棒人間)が、静止系において速度$\bf v$で直線運動する点$P$を観察する様子を表している。

静止系から点$P$を見ると、赤線に沿って直線運動するように見える。ところが、回転系の軸にいる観察者から見ると、点$P$は黄色い破線に沿った軌道を辿るように見えるだろう。このように、回転系から見ると、静止系から見たときとは点$P$の軌道がずれることになる。この軌道のずれの原因を、回転系が回っているからではなく、点$P$に「なんらかの力」が加わっているからだとしたとき、この「なんらかの力」のことをコリオリの力というのである。図中では、コリオリの力${\bf F}_C$は青い矢印で表されている。

そして、この軌道がずれる方向は、明らかに回転系が回る方向とは逆向きとなる。

以上を踏まえると、コリオリの力${\bf F}_C$は、次のように書ける。

$${\bf F}_C=-2m{\bf ω}×{\bf v}$$

コリオリの力を簡単に実感できる実験

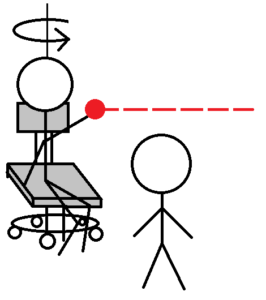
回転いすに座って回ってみる。この回転している状態で、赤いボールを前方に向かって投げる。この様子を外から見ている人から見ると、赤いボールの軌跡は上の図の赤い点線に沿って直進するようにみえる。ところが、回転いすに座っている人からそのボールを観察すると、ボールの軌道は下の黄色の点線のように、回転いすの回転方向とは逆方向にずれるはずだ。もし疑うならば実際にこの状況を再現してみればよい。

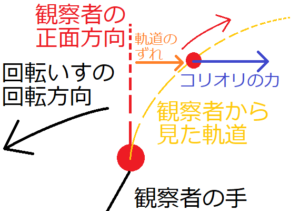
そして、ボールの軌道がずれる様子から、このボールには、上の図の青い矢印で表した力のような、回転方向とは逆方向の力が働いているとみなすことができる。この青い矢印で表した力をコリオリの力という。

実際にこの実験をすれば、コリオリの力がどのようなものか想像しやすくなるだろう。ただし、周りに十分注意してから行うようにしよう。

まとめ

・コリオリの力とは、系$S’$が系$S$に対して回転運動をしているときに発生する見かけ上の力のことである。

・コリオリの力を数式で表した。

参考文献

・戸田盛和(1982)『力学〔物理入門コース1〕』,岩波書店.

コリオリの力とは