エルステッドは19世紀に、電流が方位磁針を狂わせることを発見した。このことは、電流と磁場の間になんらかの関係があることを意味している。
この記事では、磁束密度とその向きについて考える。
目次
2つの直線電流間の力
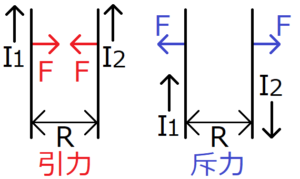
方位磁針が電流によって狂わされるということは、電流もまた磁石と同じ性質をもつと考えられる。実験事実より、距離\(R\)だけ離れる2つの平行な直線の導線について、同じ方向に進む電流には引力が、逆方向に流れる電流には斥力が働くことが知られている。さらに、単位長さ当たりの導線にかかる力の大きさ\(F\)は、次の式を満たす。
この\(F\)は正ならば引力を、負ならば斥力を表す。また、比例定数\(k\)は通常\(k=\frac{μ_0}{2π}\)と書く。この\(μ_0\)を真空中の透磁率とよぶ。
磁束密度の定義
電場をクーロン力の式を使って定義したときと同じように、磁束密度の大きさも式(1)を使って全く同じように定義できる。
直線電流\(I_1\)がつくる磁束密度の大きさ\(B(r)\)を、次のように定義する。ただし\(r\)を、電流\(I_1\)が流れる導線からの距離とする。
これを式(1)と組み合わせると、電流\(I_2\)が、磁束密度\(B\)から受ける力は次のような簡単な形で書ける。
磁束密度の向きについて
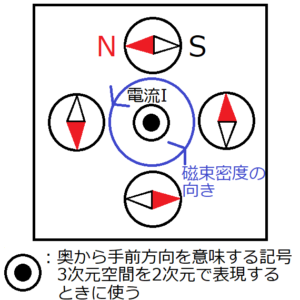
直線電流の近くに方位磁針を置いたときの、磁針の向きを調べる。上の図のように、平面に方位磁石を4つ置く。そして、その平面と垂直に交わるような、奥から手前方向に向かう電流を流す。すると、4つの方位磁石は図のような向きになる。
磁束密度の向きは、方位磁石のN極の向きと定義する。このように定義すると、直線電流と磁束密度の向きの関係は、直線電流を親指方向、磁束密度の向きを他の指方向とした右ねじの関係に対応する。
磁束密度の向きと力の向き
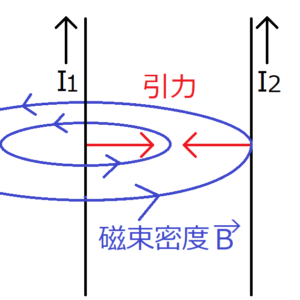
2つの直線電流が同じ方向に流れている図に、直線電流\(I_1\)がつくる磁束密度を書き込んでみる。すると、電流\(I_2\)と交わる場所の磁束密度の向きは、手前から奥の方向だとわかる。さらに、実験事実より電流\(I_2\)には、電流\(I_1\)に向かう引力が働く。
以上のことと式(2)を踏まえると、電流\({\bf I}_2\)と磁束密度\(\bf B\)、力\(\bf F\)の関係を、次のような外積で表せることに気づく。
事実、今回は磁束密度\(\bf B\)と電流\({\bf I}_2\)が直交していることに気を付けると、式(3)から式(2)が求まる。
参考:内積・外積の用途
フレミング左手の法則
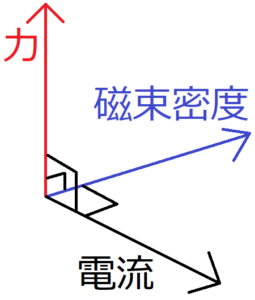
式(3)の外積に注意すると、電流\(\bf I\)と磁束密度\(\bf B\)と力\(\bf F\)の方向の関係は、上の図のようになる。これを暗記する方法として、フレミング左手の法則がある。
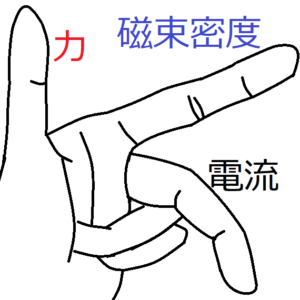
左手の中指と人差し指、親指を限界まで広げる。そして、それぞれの指に電流・磁束密度・力を当てはめる。中指から親指にかけて、当てはめる物理量の頭文字をとって、「電・磁・力」と覚えれば、指と物理量の対応関係を間違えにくいだろう。
このフレミング左手の法則を使えば、磁束密度中の電流にかかる力の向きをすぐに求められる。
磁束の定義
電気力線が電場の向きを表していたように、磁束密度にもその向きを表す線が存在する。この磁束密度の向きを表す線を磁束とよぶ。上の図の青い線が磁束を表している。
磁束\(Φ\)は、磁束密度の面積分で定義される。
まとめ
・直線電流が方位磁針の向きに干渉することから、電場と磁場には何らかの関係がある。
・2つの直線電流間の力をもとに、磁束密度と磁束を定義した。
おまけ ビオ・サバールの法則について
今回は直線電流がつくる磁束密度について考えたが、微小距離を流れる電流がつくる磁束密度を表す法則も存在する。その法則をビオ・サバールの法則とよぶ。
この法則を使えば、導線の形に依らずに、電流がつくる磁束密度を求めることができる。詳しくは下の記事を参照のこと。
参考:ビオ・サバールの法則
参考文献
・伊東敏雄(2008)『電磁気学 (朝倉物理学選書)』,朝倉書店.
・砂川重信(1987)『電磁気学 (物理テキストシリーズ 4)』,岩波書店.
・砂川重信(1988)『電磁気学―初めて学ぶ人のために』,培風館.

