1. /
  2. /
  3. 原子の構造―電子軌道と原子核について

原子の構造―電子軌道と原子核について

  • このエントリーをはてなブックマークに追加
  • LINEで送る

原子の構造を大雑把に説明すると、「原子核の周りに電子が存在しているような粒子」となる。そして原子核は陽子と中性子で成り立ち、元素の種類は陽子の数で決まる。

中学や高校で学習するのはだいたいここまでだが、この記事ではその知識をもとにもう少しだけ厳密に原子の構造を考えてみる。

「電子が原子核の周囲を回っている」は誤解の元

少し考えてみれば、電子が原子核の周りを古典的に回り続けるのは不可能であることに気づくだろう。電子が加速度運動をすると、電磁波を発生する。円運動は加速度運動のため、当然円運動する電子も電磁波を発生するはずだ。電磁波を発生するということは、電子がエネルギーを放出していると言い換えられる。ところが、もしエネルギーを放出しているならば、徐々に円軌道の半径が小さくなっていき、原子がつぶれるはずだ。ところが、実際には原子がつぶれることはない。

このことから、中学で学習したような「電子が原子核の周囲を回っている」ということの不自然さに気づく。

ド・ブロイ波という考え

そこで、ド・ブロイ波という考えが出てきた。電子を粒子と考えると上記のような不都合が生じる。それならば、電子を波として考えればしっくりくるのではなかろうか。

原子の周りにある電子を、原子半径を半径とした円周上に定在波をつくるような波として考える。この波は定在波だから、この円周上に存在し続ける。こう考えると、原子がつぶれるなどということは起きない。

シュレディンガー方程式で電子の軌道を正確に求める

存在確率とは

量子力学が発達していき、シュレディンガー方程式というものが誕生した。このシュレディンガー方程式を使うと、存在確率というものが求まる。

中学では、電子は原子核の周りを回転しているものと教えられることが多い。ところが、そもそも電子のような素粒子レベルで小さな粒子の場所を、一点の座標のみで表すことはできない。量子力学によると、電子のような素粒子の座標は絶えず変動している。そのためこの座標は、一点ではなく、粒子が存在する確率でのみ表現することができる。この確率のことを存在確率という。

参考:シュレディンガー方程式を解く意味とは

電子雲とは

電子の場所は、一点の座標のようなはっきりとした指標ではなく、存在確率というぼやけた指標でしか表現できない。つまり、存在確率が存在する場所に電子が遍在しているとも考えられる。

この電子が遍在している空間を、電子雲という。

いろいろ書いたが、要は存在確率と電子雲は似たようなものだと考えてよい。ただ電子の軌道について書くときは電子雲という表現がよく使われるため、ここでも電子雲という言葉を使う、というだけである。

電子殻と電子軌道

原子の周りに存在する電子が、原子核に近い側からK殻、L殻、M殻、N殻…という具合に電子殻を形成することは、中学でも習っただろう。一番外側の殻に存在する電子のことを最外殻電子と呼んだはずだ。そして、K殻、L殻、M殻、N殻…は、主量子数ではそれぞれ1,2,3,4…に対応している。それぞれの殻に入れる最大の電子の数は、主量子数nを使うと、2n2と表現できる。

これとは別に、電子が入る軌道というものがある。こちらは、小さい順にs軌道、p軌道、d軌道、f軌道…という具合に呼ばれる。

シュレディンガー方程式をコンピュータで解くと、それぞれの軌道ごとに下の図のような電子雲が求まる。

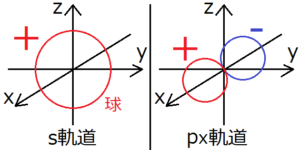
上の図ではp軌道はx方向のものしか表していないが、y方向とz方向のp軌道も向きが違うだけで形は同じである。d軌道は様々な形があるので、気になったら調べてみよう。

原子核とは

原子核とは、原子の中心に存在する粒子のことである。これは正に帯電している陽子と、正にも負にも帯電していない中性子で構成される。

陽子と中性子の質量は同じくらいだが、電子の質量は陽子･中性子の質量の約1800分の1といわれている。そのため、原子の質量のほとんどは原子核のものだといえる。陽子と中性子の数の和を質量数というが、これは電子の数を無視しても原子の質量がほとんど変わらないためである。

ちなみに、X線にはアルファ線、ベータ線、ガンマ線、中性子線が存在するが、アルファ線の正体は陽子2個中性子2個のヘリウム原子核である。

同位体とは

元素の種類は陽子の数で決まるが、同じ元素でも中性子の数が異なる場合がある。このように、同じ元素でも質量数が異なるような原子の関係を同位体とよぶ。

例えば放射性元素では、同位体で半減期が異なる。つまり放射性元素の寿命は、元素の種類だけでなく、原子核中の中性子の数にも依存するといえる。

原子核の密度

原子核の大きさは、原子の10万分の1程度といわれている。この原子核にほとんどの原子の質量が集中しているということは、原子核の密度はとんでもないことになっているだろう。

ここでは試しに質量数4のヘリウム原子核の密度を求めてみる。

原子核の半径Rと質量数Aの間には、一般的に次の関係が成り立つ。

R=1.25×10−15×A13[m]

これにA=4を代入して、原子核の体積を求める。

V=43πR3=43π(1.25×10−15×413)3≒3.27×10−44[m3]

また、質量数4のヘリウム原子1個の質量Mは

M=4.006.02×1023≒6.64×10−24[g]

だから、原子核の密度ρは次のようになる。

ρ=MV=6.64×10−243.27×10−44≒2.03×1020[g/m3]

想像しやすいように、単位を[g/m^3]から[g/cm^3]に変えてみる。

ρ≒2.03×1020106[g/cm3]=2.03×1014[g/cm3]

以上より、ヘリウム原子核の密度は1辺1cmの立方体あたり約2000億kgである。

まとめ

・電子の軌道は、古典的な物体の軌道ではなく、電子雲として考えると理解しやすい。

・原子核は、原子の質量のほとんどを持っている。そのため原子核の密度はとても大きい。

  • このエントリーをはてなブックマークに追加
  • LINEで送る

SNSでもご購読できます。

コメントを残す

*

CAPTCHA