ビオ・サバールの法則
ビオ・サバールの法則とは、位置\({\bf r}\)における、電流による磁束密度\({\bf B}\)を表す式である。この式はビオとサバールによって行われた実験によって求められたものである。
\(d{\bf s}\):電流が進む向きを表すベクトル \(I\):電流の強さ
位置\({\bf r}\)における磁束密度\({\bf B}\)を求めるには、上の式の両辺を積分すればよい。この式の右辺に含まれている微小量は\(d{\bf s}\)であるため、電流の通り道に沿って積分する。
例題 直線電流の周りの磁束密度
問題の見通し
次のように、直線電流\(I\)の周りにできる磁束密度を求める。
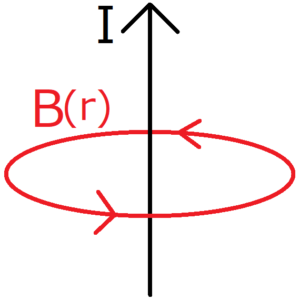
この図から、回転対称性より、磁束密度は導線からの距離のみに依存することがわかる。ここでは、導線から距離\(a\)だけ離れた地点の磁束密度\({\bf B}\)を求める。
外積の大きさはsinを使って表せたことを思い出す。
参考:内積・外積の用途
この式をビオサバールの法則に適用すると、磁束密度の大きさ\(B\)は、次のようになる。
上の式の\(r\)は、位置\({\bf r}\)から導線上の微小距離\(ds\)までの距離である。したがって、\(r\)は\(ds\)に依存する。だから、\(r\)と\(ds\)を共通の変数をもつ形に変形して、積分できるようにしなければならない。
\(θ\)は、位置\({\bf r}\)と導線が、\(ds\)で交わるときにできる角度を表す。よって、導線上で\(ds\)が動くと\(θ\)も変化する。このことも考えると、\(ds\)を\(dθ\)に変換して、さらに\(r\)を\(θ\)で表せば、ビオサバールの法則の式を問題なく積分できるようになる。
\(r\)の変形
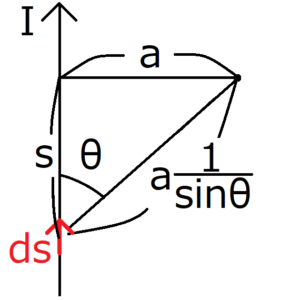
導線から距離\(a\)だけ離れている地点を考えるとき、その場所から\(ds\)までの距離\(r\)を\(θ\)を使って表すと、\(r=a\frac{1}{sinθ}\)となる。
\(ds\)の変形
上図から、次の式が成り立つ。
両辺を\(θ\)で微分すると、
$$ds=\frac{a}{sin^2θ}dθ$$
積分の計算
以上で、積分を計算する準備は整った。これまでの結果を最初のビオサバールの法則の式に代入する。導線\(S\)の範囲(\(-∞~∞\))は、角度\(θ\)の範囲(\(0~π\))に対応することに気を付ける。
以上で、電流\(I\)が流れている導線から距離\(a\)だけ離れた位置の磁束密度の大きさ\(B\)が求められた。
磁束密度の向きについては、ビオサバールの法則に含まれる外積から求まる。
まとめ
・ビオサバールの法則を使えば、電流によって発生する磁束密度を計算できる。
・ビオサバールの法則の積分は、電流が流れる導線に沿って積分すればよい。
参考文献
・砂川重信(1987)『電磁気学 (物理テキストシリーズ 4)』,岩波書店.

