ラザフォードによって原子には正に帯電した原子核が存在していたことが明らかになり、その後原子のモデルとして、原子核の周りを電子が円運動している状態が提唱された。ところが、電子は円運動すると外部に電磁波を放出するため、このモデルでは次第に電子が円運動しながら原子核に近づいていくことになる。これは原子がつぶれることを意味するが、現実的にそれはありえない。
そこで、ボーアは電子を粒子ではなく波として考えて原子モデルを考えた。つまり、原子の周りで定常波をつくるような波を電子としたのだ。このようなモデルで考えた、電子を1個のみ含む水素原子の半径のことをボーア半径という。
さらに、原子核のまわりにある電子のエネルギーが離散的であることも、ボーア半径の導出に使った式を再利用することで簡単に確認できる。
この記事では、ボーア半径と、水素原子のエネルギー準位を具体的に求める。
目次
新しい電子モデル
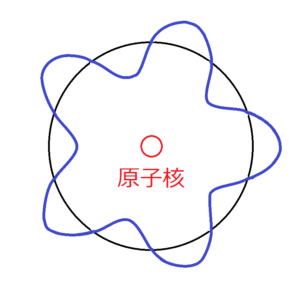
上の図は、原子の円周上に定在波を作るような波を電子としたときの原子のモデルである。図では歪んでしまったが、正確にはもっときれいな波の形をしている。
図中の青い波が電子、黒い円が電子の軌道を表している。この青い波のような、粒子を波として表した物質波のことをドブロイ波とよぶ。そしてボーア半径とは、電子が1個しかないときの水素原子の半径のことである。
ここからは、計算によってボーア半径を求めることで、水素原子の半径を考えてみる。
参考:ド・ブロイ波の例題集
水素原子の古典モデル
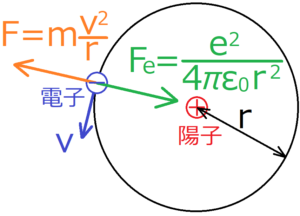
まずは、原子核の周りを電子という粒子が円運動しているという古典モデルを考える。
電子と陽子は、クーロン力によって引き寄せあう力が働く。ただし陽子の質量は電子の質量よりもはるかに大きいため、実際のところ陽子の周りを電子が回転しているだけのように見える。
電子が円運動し続けているということは、電子にはクーロン力につりあうような遠心力が働いているということになる。このことを式で表すと次のようになる。
$$m\frac{v^2}{r}=\frac{1}{4πε_0}\frac{e^2}{r^2}$$
ボーアの量子条件
電子が円運動するとき、通常は電磁波が発生する。ところがボーアは、電子が特定な条件下で円運動するときは、電子は電磁波を発生させずに円運動を続けるという仮説を立てた。そしてその条件とは、電子の角運動量が\(\frac{h}{2π}\)の自然数倍であることである。半径\(r\)の円周上を速さ\(v\)で回転する質量\(m\)の物体の角運動量は、\(mrv\)であった。これを考慮すると、ボーアの量子条件は次の式で表せる。
$$mrv=\frac{h}{2π}n \ (n:自然数)$$
ここで、\(h\)はプランク定数と呼ばれるもので、
$$h≒6.63×10^{-34}J・s$$
程度の大きさである。
ボーア半径の導出
本題のボーア半径を、下の手順に沿って求める。
まず、電子のつり合いの式の両辺に\(\frac{r^2}{mr}\)をかけて、次のように変形させる。
$$v^2=\frac{1}{4πε_0}\frac{e^2}{mr}$$
この式に、量子条件の式
$$v=\frac{h}{2πmr}n$$
を代入する。
$$\left(\frac{h}{2πmr}n\right)^2=\frac{1}{4πε_0}\frac{e^2}{mr}$$
後は原子半径\(r\)について解けばよい。
$$r=\frac{ε_0h^2n^2}{πme^2}$$
この式の右辺はすべて明らかな定数で構成されている。
\(h\)は前述したプランク定数、\(ε_0\)は真空中の誘電率、\(m\)は電子の質量、\(e\)は電子の素電荷である。また、今回は基底状態(n=1)の電子について考えることにすると、それぞれの定数に適切な値を代入すればボーア半径が求まる。
\begin{eqnarray}r&=&\frac{ε_0h^2}{πme^2}\\&≒&\frac{(8.85×10^{-12})・(6.63×10^{-34})^2}{3.14・(9.11×10^{-31})・(-1.60×10^{-19})^2}\\&≒&5.31×10^{-11}\end{eqnarray}
オングストロームについて
原子の大きさについては、よくオングストローム(Å)という単位が使われる。
$$1[Å]=10^{-10}[m]$$
1nmが\(10^{-9}\)mであるため、1Åは1nmの10分の1にあたる。
この単位を使うと、ボーア半径は次のようになる。
$$r=0.531[Å]$$
つまり、水素原子の直径はおよそ1Å程度だといえる。
水素原子のエネルギー準位の導出
次に、水素原子のエネルギー準位を求める。原子核のまわりにある電子のエネルギーは、運動エネルギーと位置エネルギーの和になる。運動エネルギーは\(\frac{1}{2}mv^2\)をもとに求められ、また位置エネルギーは電子に働く力を位置で積分すれば求められる。これ以降、それぞれを詳しく求める。
電子の運動エネルギー
運動エネルギーの式に、電子のつり合いの式で求めた\(v^2\)を代入すればよい。原子核と電子の距離\(r_n\)を使うと、運動エネルギーKは次のようになる。
電子の位置エネルギー
そもそも位置エネルギーとは、物体に働く力を位置で積分したものにマイナスをつけたものとして定義された。
$$U(r)=- \int f(r) dr$$
上の参考記事では天体の万有引力による位置エネルギーを求めているが、全く同じことを原子核のまわりの電子にも適応してみる。
電子に働くクーロン力は、水素原子の古典モデルで示したように
で与えられる。ただし、今回は原子核を極座標の原点として考えたいため、原子核方向に働くクーロン力にはマイナスをつけなければならない。したがって、これを位置\(r\)で積分すればよい。
無限遠を基準として、原子核と電子の距離\(r_n\)まで積分すると、
電子の総エネルギーとエネルギー準位
以上より、2つのエネルギーを足せば、電子の総エネルギー\(E_n\)が求まる。
ここで、式中の\(n\)は任意の自然数であった。このことから、電子のエネルギーは連続的ではなく、離散的だといえる。この式を満たす電子のエネルギーの値のことを、水素原子のエネルギー準位という。
まとめ
・水素原子の古典モデルとボーアの量子条件を組み合わせて、ボーア半径を求めた。
・水素原子の直径はおよそ1Åである。
参考文献
辻信行(2006)『なるほど量子力学〈2〉』,海鳴社.
原田勲・杉山忠男(2011)『量子力学1 (講談社基礎物理学シリーズ)』,講談社.

