完全反対称テンソルとは、テンソル解析で出てくる記号の一つである。エディントンのイプシロンやレヴィ・チヴィタの記号と呼ばれることもある。この記号はテンソル解析はもちろんのこと、量子力学や、高級な電磁気学の専門書にもよく出てくる。
この記事では、完全反対称テンソルが具体的にどのような値を取るのかを解説する。
数学
デルタ関数と使用例
[mathjax]
デルタ関数\(δ(x-a)\)とは、カッコの中が\(0\)のときのみ特殊な値になるようなものであり、次のようにして定義される。
$$\int_{-∞}^∞ f(x)δ(x-a)dx=f(a)$$
このデルタ関数は名前に関数とついているが、正確には関数ではない。そのため、このように積分を使って定義される。
内積・外積の用途
\({\bf A}=(a_x,a_y,a_z)\)、\({\bf B}=(b_x,b_y,b_z)\)
内積
\begin{eqnarray} {\bf A}･{\bf B}&=&a_xb_x+a_yb_y+a_zb_z\\&=&|{\bf A}||{\bf B}|cosθ \end{eqnarray}
外積
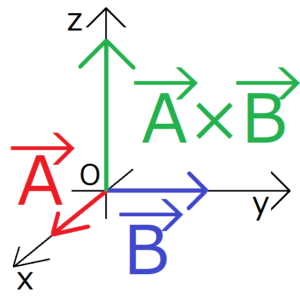
右ねじを意識すれば外積の向きを間違えない。
\begin{eqnarray} {\bf A}×{\bf B}&=&\begin{vmatrix} {\bf i}&{\bf j}&{\bf k}\\a_x&a_y&a_z\\b_x&b_y&b_z \end{vmatrix}\\&=&{\bf i}(a_yb_z-a_zb_y)+{\bf j}(a_zb_x-a_xb_z)+{\bf k}(a_xb_y-a_yb_x) \end{eqnarray}
$$|{\bf A}×{\bf B}|=|{\bf A}||{\bf B}|sinθ$$
参考:行列式の計算方法
複素積分における積分経路の設定方法
この前は定理によって複素積分を求める方法について記事にしたが、単純に定理にあてはめるだけでは解けない複素積分も存在する。ところが、そのような複素積分でも、自分で積分経路を設定することで解けるようになる。さらに、実数関数の積分を複素積分に拡張して解くこともできる。今回はこれを適用して解ける問題を見てみる。
収束半径とは何か
次のべき級数を考える。
$$\sum_{n=0}^∞ a_nz^n･･･(1)$$
このべき級数を構成する\(a_n\)と\(z\)の絶対値をとる。
$$\sum_{n=0}^∞ |a_n||z|^n･･･(2)$$
このべき級数(2)が収束することを、絶対収束という。そして、べき級数(2)が収束すれば、べき級数(1)も収束するといえる。
収束半径Rとは、べき級数(2)が絶対収束する\(|z|\)と発散する\(|z|\)の境界を指す。もし\(|z|<R\)ならばべき級数(1)は収束し、\(|z|>R\)ならばべき級数(1)は発散する。\(|z|=R\)のときはべき級数ごとに収束・発散が異なるため、問題ごとに収束するか発散するか考える必要がある。
ラプラス変換と代数方程式
ラプラス変換とは、下のような変換\(F(s)\)を指す。
$$F(s)=\int_0^∞ f(t)e^{-st}dt$$
ラプラス変換前の関数\(f(t)\)は\(t\)に依存している関数であるが、ラプラス変換後の関数\(F(s)\)は\(s\)に依存している関数になっている。
固有値・固有ベクトルの求め方
行列\({\bf A}\)の固有値λと固有ベクトルφは、次の関数を満たす。
$${\bf A}φ=λφ$$
この固有値λと固有ベクトルφの求め方を見ていこうと思う。
定理による複素積分の解き方まとめ
複素積分の解き方は、コーシーの積分定理や留数定理を利用するものや、自分で特定の積分経路を指定するものなど、様々な種類がある。問題を解くときはそれらを適切に使い分けなければいけないが、すべての方法が頭に入っていなければ土俵に上がることすらもできない。この記事では、定理を使う複素積分の解き方のパターンをまとめてみようと思う。
この記事では以前紹介した「正則」という単語が重要になるため、先にコーシー・リーマンの方程式の記事を読むことをお勧めする。
コーシー・リーマンの方程式と正則
複素関数\(f(z)\)が範囲\(D\)で複素微分ができるとき、複素関数\(f(z)\)は範囲\(D\)で正則であるという。
ここで、\(f(z)=u(x,y)+iv(x,y)\)(ただし\(z=x+iy\)で、かつ\(u(x,y)\),\(v(x,y)\),\(x\),\(y\)はすべて実数)とすると、下の2つの方程式をまとめてコーシー・リーマンの方程式と呼ぶ。
$$\frac{∂u(x,y)}{∂x}=\frac{∂v(x,y)}{∂y}$$
$$\frac{∂u(x,y)}{∂y}=-\frac{∂v(x,y)}{∂x}$$
\(u(x,y)\)と\(v(x,y)\)が上のコーシー・リーマンの方程式を満たすとき、複素関数\(f(z)\)は正則であるといえる。
続きを読む
フーリエ変換
フーリエ変換
$$F(k)=\int_{-∞}^{∞} f(x)e^{-ikx} dx$$
逆フーリエ変換
$$f(x)=\frac{1}{2π}\int_{-∞}^{∞} F(k)e^{ikx} dk$$
波が関数\(f(x)\)で与えられるとする。それをフーリエ変換すると、波\(f(x)\)を波数\(k\)の関数\(F(k)\)として表すことができる。\(F(k)\)は、\(f(x)\)に含まれる波を波数\(k\)ごとに分解して、それぞれの波の大きさを関数として表したものである。フーリエ変換すれば波\(f(x)\)を\(F(k)\)に変換できるし、逆フーリエ変換すれば\(F(k)\)を波\(f(x)\)に変形できる。
12