なぜE=hνが成立するのか

重要なお知らせあなたのWebブラウザーでJavaScriptを有効にする方法

$E=hν$

この式は、光の振動数 $ν$ とエネルギー $E$ の関係式である。 $h$ はプランク定数で、次の定数となっている。

$h≒6.63×10^{-34} [m^2kg/s]$

この式は量子力学で最初に出てくる重要な公式であり、量子力学の勉強はここから始まると言っても過言ではない。電子のエネルギー準位が落ちたときには、その落ち幅に対応した振動数の光が放出されることになる。この式はその光の振動数の計算に非常に役に立つ。

この記事では、なぜ上の式が成立するのかを考える。

目次 [hide]

1 熱せられた物体から放出される電磁波の振動数について
2 プランクの式の導出
3 量子仮説のその後
- - 3.0.1 光量子仮説の式
4 まとめ
5 参考文献

熱せられた物体から放出される電磁波の振動数について

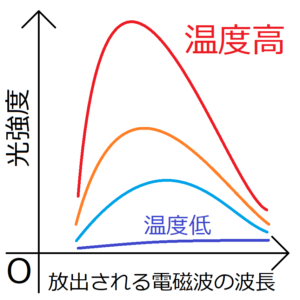
金属などの物体を熱すると、その熱した物体自身から電磁波が放出される。この電磁波の振動数は、図のように物体の温度が上がるにつれて大きくなっていく傾向がみられる。

物体の温度ごとの電磁波の強度と振動数の関係を表す曲線を数式化する試みは、プランク以前には、ウィーンやレイリー･ジーンズによってなされていた。ただし、ウィーンが作った式では $\frac{ν}{T}$ が小さい領域では実験値と合わず、またレイリー･ジーンズの式は $\frac{ν}{T}$ が大きい領域で実験値と合わなくなる。つまり、一つの数式だけでこれらの曲線を正確に表現できていなかったのだ。

ところがプランクは、両者の公式の近似を用いて、 $\frac{ν}{T}$ にかかわらずに実験値によく合う式を考えることに成功した。その式のことをプランクの放射公式と呼び、具体的には次の式となる。

$F(ν,T)=\frac{8πh}{c^3}\frac{ν^3}{e^{\frac{hν}{kT}}-1}$

ここで、電磁波のエネルギー $ε_n$ と振動数 $ν$ の間に次の関係が成り立つという仮定が前提となって、上の式が成り立っていることに注意する。

$ε_n=nhν$

ここで、nは整数である。では、これからこのプランクの式を、上の関係が成り立つことを仮定して求めてみる。

プランクの式の導出

電磁波のエネルギーについて

カノニカル分布とは、系のエネルギーが特定のエネルギー $ε_σ$ となる確率 $p_σ$ に関する確率分布のことで、数式を使うと次のように表される。

$p_σ=\frac{1}{\displaystyle \sum_σ e^{-\frac{1}{k_BT}ε_σ}}e^{-\frac{1}{k_BT}ε_σ}$

参考:分配関数とカノニカル分布の導出

この分布を使うと、電磁波の平均エネルギー<ε>が求まる。 $ε_n=nhν$ という量子仮説を導入すると、振動数 $ν$ の電磁波のエネルギーの平均は次のようになる。期待値の求め方に似ていることに気づけばわかりやすいだろう。

$\begin{eqnarray}<ε>&=&\sum_{n=0}^∞ ε_np_n\\&=&\sum_{n=0}^∞ \left[ ε_n\frac{1}{\displaystyle \sum_{m=0}^∞ e^{-\frac{1}{k_BT}ε_m}}e^{-\frac{1}{k_BT}ε_n} \right] \\&=&\sum_{n=0}^∞ \left[ nhν e^{-\frac{1}{k_BT}nhν}\right] \frac{1}{\displaystyle \sum_{m=0}^∞ e^{-\frac{1}{k_BT}mhν}} \\&=&hν\sum_{n=1}^∞ \left[ n\left(e^{-\frac{hν}{k_BT}}\right)^n \right] \frac{1}{\displaystyle \sum_{m=0}^∞ \left( e^{-\frac{hν}{k_BT}}\right)^m }\\&=&hν \frac{e^{-\frac{hν}{k_BT}}}{\left( 1-e^{-\frac{hν}{k_BT}} \right)^2} \left( 1-e^{-\frac{hν}{k_BT}}\right)\\&=&hν \frac{e^{-\frac{hν}{k_BT}}}{1-e^{-\frac{hν}{k_BT}}}\\&=&\frac{hν}{e^{\frac{hν}{k_BT}}-1} \end{eqnarray}$

上の4行目の変形について、n=0の場合は項全体が0になるため、n=1から和を考えても結果は同じである。また、5行目について、2つの無限級数の有名な公式を使った。

$\displaystyle \sum_{n=0}^∞ x^n=\frac{1}{1-x}$

$\displaystyle \sum_{n=1}^∞ nx^n=\frac{x}{(1-x)^2}$

上の2式はどちらも

$0<x<1$

が前提となっていることに注意する。これらの導出は検索すればすぐに出てくるため、ここでは割愛する。

ともかく、カノニカル分布を使って振動数νの電磁波のエネルギーの平均エネルギーを求められた。

立方体中の固有振動について

1次元の固有振動とは

物体ごとに振動しやすい振動数というものがあるが、その振動しやすい振動数のことを固有振動数という。この記事における1次元の固有振動とは、有限の長さの弦上に定在波を作るような波の振動数のことを指す。

長さ $L$ の弦を固定端で振動させたときには、次の条件を満たす定在波が形成される。

$\frac{1}{2}nλ=L$

ここで、波長λと振動数νの間には、波の速度cを使って次のような有名な関係があった。

$c=νλ$

この式をλについて解いて、上の定在波が満たす条件の式に代入すると、長さLの弦に現れる定在波の振動数が求まる。

$ν=\frac{nc}{2L}$

3次元の固有振動とは

以上のことを、3次元の立方体中の電磁波にも拡張してみよう。ここでいう波の速度cとは電磁波の速度、つまり光速ということになる。

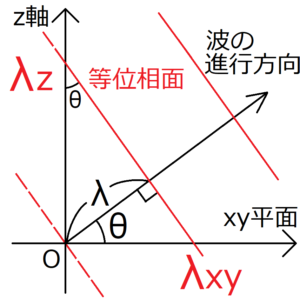
上の図は、縦軸にz軸、横軸にxy平面をとった立方体の図である。立方体中の電磁波は壁を固定端として振動する。

電磁波の等位相面のz軸･xy平面のそれぞれの切片をとると、それぞれの軸･平面における定在波のz軸方向成分の波長 $λ_z$ と、xy平面上の波長 $λ_{xy}$ が求まる。そしてこれらは三角関数を使って次のように求まる。

$λ_z=\frac{λ}{sinθ}$

$λ_{xy}=\frac{λ}{cosθ}$

それぞれを変形させて、次の式を得る。

$sinθ=\frac{λ}{λ_z}$

$cosθ=\frac{λ}{λ_{xy}}$

上の式を、有名な公式

$1=cos^2θ+sin^2θ$

に代入する。

$1=\left(\frac{λ}{λ_z}\right)^2+\left(\frac{λ}{λ_{xy}}\right)^2$

両辺をλで割る。

$\frac{1}{λ^2}=\frac{1}{λ_z^2}+\frac{1}{λ_{xy}^2}$

全く同じことをx軸とy軸に対して行うことで、次の式を得る。

$\frac{1}{λ_{xy}^2}=\frac{1}{λ_x^2}+\frac{1}{λ_y^2}$

以上の式をまとめて、さらに $c=νλ$ を代入する。

$ν^2=ν_x^2+ν_y^2+ν_z^2$

また、一辺の長さが $L$ の立方体中にx軸に平行な定在波ができる振動数の条件は

$ν_x=\frac{n_xc}{2L}$

であった。y軸とz軸方向の定在波でも同じことがいえる。これらのことから、振動数空間(座標軸を $ν_x,ν_y,ν_z$ とした座標空間のこと)において、固有振動数はx軸･y軸･z軸方向にそれぞれ $\frac{c}{2L}$ 間隔で現れることがいえる。

これ以降、振動数空間における固有振動数について考える。

振動数空間の球殻

振動数空間の原点を中心とした、半径νからdνまでの球殻に含まれる固有振動数の数について考える。

この球殻の体積 $V$ は次のようになる。

$\begin{eqnarray}V&=&\frac{4}{3}π(ν+dν)^3-\frac{4}{3}πν^3\\&=&\frac{4}{3}π[ν^3+3ν^2dν+3ν(dν)^2+(dν)^3]-\frac{4}{3}πν^3\\&=&\frac{4}{3}π[3ν^2dν+3ν(dν)^2+(dν)^3]\\&≒&4πν^2dν\end{eqnarray}$

$dν$ は $1$ と比べて十分小さいため、 $dν$ が2乗以上となっている項は無視した。

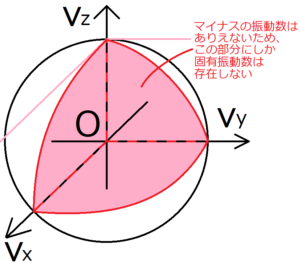
ただし、ここでは振動数は決して負にならないため、 $ν_x,ν_y,ν_z$ のすべてが正となっている範囲にのみ固有振動数が存在する。だから、求めた球殻の体積のうち、固有振動数が存在する割合は $V/8$ である。

したがって、振動数が $ν$ から $dν$ の範囲にある固有振動数の数は、次のように求められる。

$\begin{eqnarray}G(ν,T)dν&=&4πν^2dν･\frac{1}{\left(\frac{c}{2L}\right)^3}･\frac{1}{8}×2\\&=&\frac{8πν^2L^3}{c^3}dν\end{eqnarray}$

最後の $×2$ は、電磁波の偏光自由度が2であることを反映している。

以上で、本題のプランクの式を導出する準備ができた。

プランクの式の導出

上では、振動数 $ν$ の電磁波のエネルギーの期待値と、長さ $L$ の立方体中に存在できる電磁波の振動数の数を求めた。つまり、この2つをかけると、その立方体中の電磁波の総エネルギーの期待値が求まる。

$\begin{eqnarray}G(ν,T)<ε>&=&\frac{8πν^2L^3}{c^3}･\frac{hν}{e^{\frac{hν}{k_BT}}-1}\\&=&\frac{8πhL^3}{c^3}･\frac{ν^3}{e^{\frac{hν}{k_BT}}-1}\end{eqnarray}$

ただし、上で求められたのは、あくまで立方体 $L$ 中の電磁波に関する式である。そこで、その立方体の体積 $L^3$ で両辺を割れば、単位体積あたりの電磁波のエネルギーが求まる。

$F(ν,T)=\frac{8πh}{c^3}\frac{ν^3}{e^{\frac{hν}{kT}}-1}$

以上でプランクの式が導出できた。

こうして求められたプランクの式は、実験で得られた結果とよく一致する。そのため、最初に出てきた電磁波のエネルギーが量子的なものであるという仮説

$ε_n=nhν$

も正しいという認知が広まっていったのだ。

量子仮説のその後

プランクは量子仮説の式を提唱したが、その式自体については深く考察しなかったようだ。そのかわりにアインシュタインが、量子仮説を利用して、光量子仮説というものを考えついた。

プランクの量子仮説は、「振動数 $ν$ の電磁波のエネルギー $ε$ は、 $hν$ の整数倍にしかならない」ということを示した。そこでアインシュタインは、電磁波を一つの粒子と考えて、その粒子のエネルギーが $hν$ であるとみなせるのではないかと考えた。つまり、 $hν$ が電磁波のエネルギーの最小単位なのである。

光量子仮説の式

これまでのことを踏まえて、光量子仮説の式を書く。電磁波を１つの粒子と考えて、そのエネルギーを $E$ とする。この電磁波の振動数を $ν$ とおくとき、次の関係が成り立つ。

$E=hν$

以上が、E=hνが出てくる過程である。

まとめ

・プランクの量子仮説

$ε_n=nhν$

に基づいたエネルギー密度は、実験結果とよく一致する。したがって、この量子仮説は正しいと考えられている。

・アインシュタインは、プランクの量子仮説をもとに、光量子仮説を提唱した。

参考文献

朝永振一郎(1969)『量子力学I』,みすず書房.

原田勲･杉山忠男(2011)『講談社基礎物理学シリーズ6 量子力学I』,講談社.

なぜE=hνが成立するのか

熱せられた物体から放出される電磁波の振動数について