ジュールの法則
ジュールの法則の微分形
\(w\):単位体積内かつ単位時間で発生する熱量 \({\bf j}\):電流密度 \({\bf E}\):電場
ジュールの法則の導出
電荷\(e\)を帯びた粒子を、低電位の点\(P\)から高電位の点\(Q\)まで移動させるのにもエネルギーが要る。これに必要な仕事を\(W\)とおくと、次の関係を満たす。
したがって、逆に高電位の点\(Q\)から低電位の点\(P\)へ動く電荷は、外部に仕事\(W\)をすることになる。
強さ\(I\)の電流は、単位時間あたりで電荷\(I\)を運ぶから、単位時間当たりに電流がする仕事\(W\)は、
オームの法則\(Δφ=RI\)を代入すると、
前述したとおりに、電荷\(e\)は高電位から低電位へ動くと外部に仕事をするから、電流の仕事\(W\)が熱として外部に放出されることになる。ここで発生した熱をジュール熱と呼ぶ。また、上式のように、仕事\(W\)を電位差\(Δφ\)、抵抗\(R\)、電流\(I\)を使って表した法則をジュールの法則という。
ジュールの法則の微分形の導出
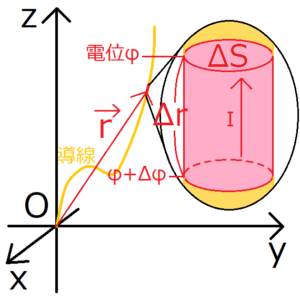
オームの法則の微分形の導出と同じように、底面積が\(ΔS\)、長さが\(Δx\)の微小円筒を考える。そしてこの微小円筒内で、単位時間かつ単位体積あたりで発生する熱量を\(w\)とする。
電流は電位が高い場所から低い場所へ流れる。言い換えると、電流が流れる向きと電位が上がる方向は逆向きだといえる。これに加えて\(W=w×(体積)\)、\(I=jΔS\)も考慮すると、通常のジュールの法則から次の式を得る。
両辺を\(ΔSΔx\)で割って、
$$w=-j\frac{Δφ}{Δx}$$
\({\bf E}=-∇φ\)を導入すると、
$$w=jE$$
後はこれをベクトル形式で表現すればよい。微小円筒の位置を\({\bf r}\)とすると、
これで、ジュールの法則の微分形が求められた。導線全体を\({\bf r}\)で線積分すれば、導線全体で発生するジュール熱を求められる。この導出は、オームの法則の微分形のものと似ているので、一度比較してみよう。
参考文献
・砂川重信(1987)『電磁気学 物理テキストシリーズ4』,岩波書店.

