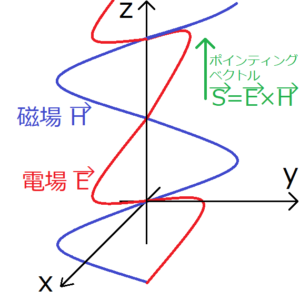
ポインティングベクトル\({\bf S}(t,{\bf r})\)とは、電磁場の流れを表すものであり、次のように定義される。
$${\bf S}({\bf r},t)={\bf E}({\bf r},t)×{\bf H}({\bf r},t)$$
ポインティングベクトルの導出
エネルギー保存則
静電場のエネルギー
位置\({\bf r}\)でのエネルギー密度は\(\frac{1}{2}ε_0{\bf E}^2({\bf r})\)で与えられるため、これを体積で積分すれば、その体積中での静電場のエネルギー\(U_e\)が求められる。
$$U_e=\frac{1}{2}ε_0 \int_V {\bf E}^2({\bf r}) d^3r$$
マクスウェル方程式
次の2つのマクスウェル方程式を思い出す。
$$rot {\bf E}({\bf r},t)=-\frac{∂{\bf B}({\bf r},t)}{∂t}$$
$$rot {\bf H}({\bf r},t)-\frac{∂{\bf D}({\bf r},t)}{∂t}={\bf j}({\bf r},t)$$
参考:Maxwell方程式の微分形と積分形
1つ目の方程式の両辺には磁場\({\bf H}\)、2つ目の方程式の両辺には電場\({\bf E}\)の内積をとる。
$${\bf H}・(rot {\bf E})=-{\bf H}・\frac{∂{\bf B}}{∂t}$$
$${\bf E}・(rot {\bf H})-{\bf E}・\frac{∂{\bf D}}{∂t}={\bf E}・{\bf j}$$
上の式から下の式を引く。
$${\bf H・}(rot {\bf E})-{\bf E}・(rot {\bf H})+{\bf E}・\frac{∂{\bf D}}{∂t}=-{\bf H}\frac{∂{\bf B}}{∂t}-{\bf E}・{\bf j}・・・(1)$$
ここで、次のベクトルの恒等式を導入する。
$$∇・({\bf A}×{\bf B})={\bf B}・(∇×{\bf A})-{\bf A}・(∇×{\bf B})$$
この恒等式を式(1)に適応すると、
$$∇・({\bf E}×{\bf H})=-{\bf E}・{\bf j}-{\bf H}・\frac{∂{\bf B}}{∂t}-{\bf E}・\frac{∂{\bf D}}{∂t}$$
\({\bf D}=ε_0{\bf E}\)、\({\bf B}=μ_0{\bf H}\)をこの式の右辺に代入する。
\begin{eqnarray} -{\bf H}・\frac{∂{\bf B}}{∂t}-{\bf E}・\frac{∂{\bf D}}{∂t}&=&-μ_0{\bf H}・\frac{∂{\bf H}}{∂t}-ε_0{\bf E}・\frac{∂{\bf E}}{∂t}\\&=&-\frac{1}{2}\left( μ_0\frac{∂{\bf H}}{∂t}・{\bf H}+μ_0{\bf H}・\frac{∂{\bf H}}{∂t}+ε_0\frac{∂{\bf E}}{∂t}・{\bf E}+ε_0{\bf E}・\frac{∂{\bf E}}{∂t} \right)\\&=&-\frac{1}{2}\frac{∂}{∂t}\left( μ_0{\bf H}・{\bf H}+ε_0{\bf E}・{\bf E}\right)\\&=&-\frac{1}{2}\frac{∂}{∂t}\left( {\bf H}・{\bf B}+{\bf D}・{\bf E}\right) \end{eqnarray}
この変形より、
$$∇・({\bf E}×{\bf H})=-{\bf E}・{\bf j}-\frac{1}{2}\frac{∂}{∂t}\left( {\bf H}・{\bf B}+{\bf D}・{\bf E}\right)$$
この式の両辺を体積積分する。
$$\int _V∇・({\bf E}×{\bf H}) dV=-\int _V {\bf E}・{\bf j}dV-\int _V\frac{1}{2}\frac{∂}{∂t}\left( {\bf H}・{\bf B}+{\bf D}・{\bf E}\right)dV$$
右辺について
まず右辺の第一項\(-\int _V {\bf E}・{\bf j}dV\)について考える。
単位体積かつ単位時間で発生するジュール熱\(w\)は、次のように与えられた。
$$w({\bf r})={\bf j}({\bf r})・{\bf E}({\bf r})$$
参考:ジュールの法則とその微分形の導出
ジュール熱\(w\)がこのように与えらえるから、これを体積積分してマイナスをつけた\(-\int _V {\bf E}・{\bf j}dV\)は、単位時間における領域\(V\)内から出て行ったジュール熱を表す。
また、右辺の第二項に含まれる\(-\frac{1}{2}\int _V{\bf D}・{\bf E}dV\)は、最初に見た静電場のエネルギーの式そのものである。このことから第二項は、単位時間での領域\(V\)内の電磁場のエネルギーの減少量を表すと考えられる。
左辺について
左辺にガウスの発散定理を適応する。
\begin{eqnarray} \int _V∇・({\bf E}×{\bf H}) dV&=&\int _S ({\bf E}×{\bf H}) d{\bf S}\\&=&\int _S ({\bf E}({\bf r})×{\bf H}({\bf r}))・{\bf n}({\bf r}) dS \end{eqnarray}
右辺の考察と組み合わせると、左辺は、単位時間で領域\(V\)を囲む面積領域\(S\)を通って出て行った電磁場のエネルギーを表すといえる。
ポインティングベクトルの定義
以上の考察から、次のようなベクトルを定義する。
$${\bf S}({\bf r})={\bf E}({\bf r})×{\bf H}({\bf r})$$
このベクトル\({\bf S}\)はポインティングベクトルといい、単位時間で、\({\bf E}\)と\({\bf H}\)に垂直な単位面積を通って外部に流れる電磁場のエネルギーを指す。これの向きは当然電磁場のエネルギーが流れる方向を向き、大きさは流れる電磁場のエネルギーの大きさを表す。
ポインティングベクトルの大きさ
平面電磁波
$${\bf E}=Ecos({\bf k}・{\bf r}-ωt)$$
$${\bf B}=Bcos({\bf k}・{\bf r}-ωt)$$
のポインティングベクトルの大きさを求めよう。
ファラデーの電磁誘導の法則
$$\frac{∂{\bf B}({\bf r},t)}{∂t}=-rot {\bf E}({\bf r},t)$$
に、上の平面電磁波を代入する。
$$ω{\bf B}={\bf k}×{\bf E}$$
この式を\(\bf B\)について解く。ここで、波数ベクトルと平行な単位ベクトルを\(\hat{\bf k}\)、波数ベクトルの大きさを\(k\)とする(つまり\({\bf k}=k\hat{\bf k}\))。
\begin{eqnarray}{\bf B}&=&\frac{1}{ω}{\bf k}×{\bf E}\\&=&\frac{k}{ω}\hat{\bf k}×{\bf E}\\&=&\frac{1}{c}\hat{\bf k}×{\bf E}\end{eqnarray}
ここで、平面波の分散関係\(ω=ck\)を使った。
参考:等位相面と平面波とは
この\(\bf B\)を、ポインティングベクトルの定義式に代入する。
\begin{eqnarray}{\bf S}&=&\frac{1}{μ}{\bf E}×{\bf B}\\&=&\frac{1}{cμ}{\bf E}×(\hat{\bf k}×{\bf E})\\&=&\frac{1}{cμ}({\bf E}^2\hat{\bf k}-(\hat{\bf k}・{\bf E}){\bf E})\\&=&\frac{\sqrt{εμ}}{μ}((Ecos({\bf k}・{\bf r}-ωt))^2\hat{\bf k}-0・{\bf E})\\&=&\sqrt{\frac{ε}{μ}}(Ecos({\bf k}・{\bf r}-ωt))^2\end{eqnarray}
電場は進行方向に対して垂直に振動する縦波だから、\(\hat{\bf k}・{\bf E}=0\)となることを途中で使った。
このポインティングベクトルの時間平均と絶対値をとる。
$$|\bar{\bf S}|=\sqrt{\frac{ε}{μ}}|E|^2$$
以上で、時間平均したポインティングベクトル絶対値が求められた。
まとめ
・ポインティングベクトルは、電磁波のエネルギーの向きと大きさを表す。
・時間平均したポインティングベクトルの絶対値を求めた。
参考文献
・川田善正(2014)『はじめての光学』,講談社.
・砂川重信(1987)『物理テキストシリーズ4 電磁気学』,岩波書店.


