波動方程式を弦の振動から導出してみた

重要なお知らせあなたのWebブラウザーでJavaScriptを有効にする方法

通常、連続的な物体の運動を考えるときは、その物体を細かく分解して考える。今回考える弦の振動も例外ではない。

今回は、弦の運動が一次元の波動方程式を満たすことを示す。

1 弦の設定
- 1.1 弦の分割
2 弦ABにかかる力
3 弦ABの動き
4 運動方程式の構築
- 4.1 角度$θ$を変位$z$で表す
- 4.2 波動方程式の導出
5 まとめ
6 参考文献

弦の設定

弦の分割

上図のような、変位が小さい弦の振動を考える。張力(弦を両側から引っ張る力)は$T$とおく。まず、弦の一部分に注目してみる。

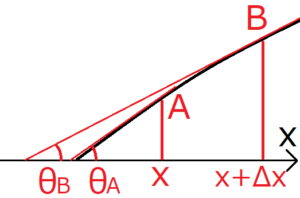
x軸を基準にして弦を分割する。まず、x軸上の任意の点$x$から微小距離だけ離れた地点$x+Δx$までの範囲に注目する。点$x$における弦の位置を$A$、点$x+Δx$における弦の位置を$B$とおく。さらに、点$A$での弦の接線とx軸がつくる角度を$θ_A$、点$B$での弦の接線とx軸がつくる角度を$θ_B$とおく。

接線に注目する理由は、弦ABにかかる張力はそれぞれの点の接線方向にかかるからだ。

弦ABにかかる力

点Aにかかる力

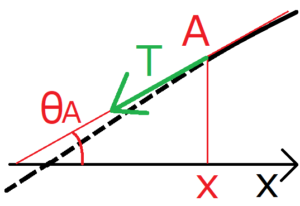
弦ABにかかる張力を成分ごとに考えるために、まず点Aにかかる力を考える。点Aでの弦の接線方向に張力がかかると考えれば、張力$T$は図のような方向にかかることになる。したがって、この張力$T$は、x軸に水平な方向の力$F_{A//}$と、x軸に垂直な方向の力$F_{A⊥}$に分解される。そしてそれらは$θ_A$を使って次のように表現できる。

$$F_{A//}=-Tcosθ_A$$

$$F_{A⊥}=-Tsinθ_A$$

張力$T$は、x軸方向と変位方向とは逆向きになっている。だから、$F_{A//}$と$F_{A⊥}$の両方にマイナスがつく。

点Bにかかる力

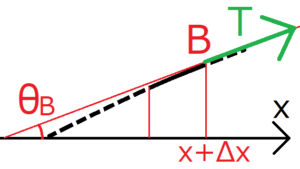
点Bにかかる力も、点Aと同様にして求められる。ただし、x軸方向かつ上方向に$T$が向いているため、$F_{B//}$と$F_{B⊥}$は正になる。

$$F_{B//}=Tcosθ_B$$

$$F_{B⊥}=Tsinθ_B$$

両方の力の和

以上から、弦ABにかかる方向別の力は、次のようになる。

\begin{eqnarray} F_{//}&=&F_{A//}+F_{B//}\\&=&-Tcosθ_A+Tcosθ_B \end{eqnarray}

\begin{eqnarray} F_{⊥}&=&F_{A⊥}+F_{B⊥}\\&=&-Tsinθ_A+Tsinθ_B \end{eqnarray}

弦ABの動き

x軸方向の力

今は変位が小さい運動を考えているため、$θ_A<<1$、$θ_B<<1$である。したがって、cosをテイラー展開すると、次の近似が成り立つ。

\begin{eqnarray} cosθ_A&=&1-\frac{θ_A^2}{2!}+\frac{θ_A^4}{4!}- \cdots \\&≒&1-\frac{θ_A^2}{2} \end{eqnarray}

$$cosθ_B≒1-\frac{θ_B^2}{2}$$

これを$F_{//}$の式に代入する。

\begin{eqnarray} F_{//}&=&-Tcosθ_A+Tcosθ_B\\&≒&-T\left( 1-\frac{θ_A^2}{2} \right)+T\left( 1-\frac{θ_B^2}{2} \right)\\&=&\frac{T}{2}(θ_A^2-θ_B^2) \end{eqnarray}

上下方向の力

sinも同様にして、次のように近似する。

\begin{eqnarray} sinθ_A&=&θ_A-\frac{θ_A^3}{3!}+\frac{θ_A^5}{5!}- \cdots \\&≒&θ_A \end{eqnarray}

$$cosθ_B≒θ_B$$

これを$F_{⊥}$の式に代入する。

\begin{eqnarray} F_{⊥}&=&-Tsinθ_A+Tsinθ_B\\&≒&-Tθ_A+Tθ_B\\&=&T(θ_B-θ_A) \end{eqnarray}

両方の力の比較

$θ_A,θ_B<<1$より、$θ_A^2<<θ_A$、$θ_B^2<<θ_B$である。したがって、次の式が成り立つ。

$$|θ_B-θ_A|>>\left| \frac{θ_A^2-θ_B^2}{2} \right|$$

この式から、x軸に平行方向の力よりも、x軸に垂直方向の力の方がはるかに大きいことがわかる。これ以降、水平方向の力は無視し、垂直方向の力のみを考える。

運動方程式の構築

弦の垂直方向の変位を$z(x,t)$、弦の線密度(単位長さあたりの質量)を$ρ$とする。これらのパラメータと垂直方向の力$F_{⊥}$を組み合わせて、$m\ddot{z}=F_⊥$に当てはめれば、次の運動方程式を得る。

$$(ρΔx)\frac{∂^2z}{∂t^2}=T(θ_B-θ_A) $$

ここで、$(θ_B-θ_A)$を変位$z(x,t)$で表せれば、この式をすっきりさせられそうだ。

角度$θ$を変位$z$で表す

点$A$における接線の傾き$z’$は、変位$z$を$x$で偏微分したものとなる。

$$z'(x,t)=\frac{∂z}{∂x}$$

また、接線の傾きはtanを使っても表せる。$θ<<1$で$tanθ≒θ$という近似を使うと、

$$z'(x,t)=tanθ_A≒θ_A$$

$$z'(x+Δx,t)=tanθ_B≒θ_B$$

これを、上の運動方程式の右辺に作用させると、

\begin{eqnarray} T(θ_B-θ_A)&≒&T(z'(x+Δx,t)-z'(x+,t))\\&=&T\frac{z'(x+Δx,t)-z'(x+,t)}{Δx}Δx \end{eqnarray}

高校で学習した微分の定義より、$Δx→0$ならば、$\frac{z'(x+Δx,t)-z'(x,t)}{Δx}→\frac{∂^2z}{∂x^2}$だから、

$$T(θ_B-θ_A)≒T\frac{∂^2z}{∂x^2}Δx$$

あとはこれを運動方程式の右辺に代入すればよい。

$$(ρΔx)\frac{∂^2z}{∂t^2}=T\frac{∂^2z}{∂x^2}Δx$$

波動方程式の導出

上で求めた式の両辺を$ρΔx$で割ると、求めたい式が現れる。

$$\frac{∂^2z}{∂t^2}=\frac{T}{ρ}\frac{∂^2z}{∂x^2}$$

$v^2≡\frac{T}{ρ}$とおくと、

$$\frac{∂^2z}{∂t^2}=v^2\frac{∂^2z}{∂x^2}$$

以上で、一次元の波動方程式が求められた。

$v^2≡\frac{T}{ρ}$より、張力$T$が大きく、線密度$ρ$が小さいほど、波が伝わる速さが速くなる。

まとめ

微小の長さの弦に加わる力から、波動方程式を求めた。

参考文献

・長谷川修司(2009)『講談社基礎物理学シリーズ2 振動・波動』,講談社.

波動方程式を弦の振動から導出してみた

弦の設定

弦の分割