[mathjax]
目次
反射の法則
$$θ_{in}=θ_r$$
屈折の法則(スネルの法則)
$$n_{in}sin{θ_{in}}=n_tsin{θ_t}$$
この記事では、平面波が上の2つの法則を満たすことを示す。
スネルの法則の導出
波の屈折と位相差について
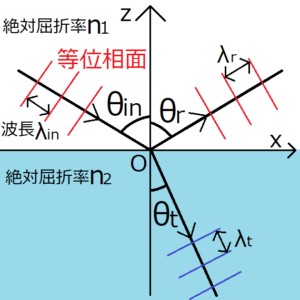
入射角\(θ_{in}\)で物体に入射する平面波を考える。黒い矢印は平面波が進む方向を表しているため、等位相面はこの矢印に対して垂直になる。
参考:等位相面と平面波とは
入射波、反射波、透過波の波動関数をそれぞれ\(ψ_{in},ψ_r,ψ_t\)とおく。
入射波、反射波、透過波は、すべて直線\(z=0\)上で交わる。この\(z=0\)上ですべての波が連続でないといけないから、直線\(z=0\)上におけるすべての波の位相は等しくなる。
すべての式に\(ωt\)を加える。
入射波・反射波・透過波の波数ベクトルについて
式(1)中の3つの\({\bf r}\)はすべて同じであることに注目する。これによって、入射波・反射波・透過波の波数ベクトルの各成分はそれぞれ等しくなることがわかる。
今、入射波は\(xz\)平面上を通る場合を考えているから、入射波の波数ベクトルのy軸方向成分\(k_{iny}\)は0になる。だから、式(3)より、反射波と透過波の波数ベクトルのy軸方向成分も0になるといえる。
この式(4)は、入射波・反射波・透過波がすべて\(xz\)平面上にあることを意味している。
x軸方向の波数ベクトル
入射波の波数ベクトルの大きさ\(k_{in}\)と、この波数ベクトルのx軸方向の大きさ\(k_{inx}\)は、上の図から次のように書けることがわかる。
反射波・透過波でも同様の関係が求まる。
式(5),(6),(7)を式(2)に代入する。
反射の法則と屈折の法則
平面波の分散関係は、次の式で表された。
参考:等位相面と平面波とは
この分散関係を式(8)に代入する。入射波、反射波、透過波では角振動数は共通だから、代入後の式を角振動数\(ω\)で割ってみる。
ここで、入射波と反射波は同じ物質中を通っているから、入射波と反射波の速さは同じになる。このことと式(9)を考慮すると、次の式を得る。
\(θ_{in},θ_{r}\)は両方とも0°よりも大きく90°よりも小さいから、
この式は、入射角と反射角が等しいことを表す。この法則を反射の法則という。
また、入射波と透過波の関係について、式(9)を変形することで次の式が求まる。
上の式ように定義された\(n\)を、入射波側の物質に対する透過波側の物質の相対屈折率とよぶ。
絶対屈折率と相対屈折率
真空中の光速を\(c\)とすると、速度\(v_a\)で波が進む物質\(a\)の屈折率\(n_a\)は、次のように定義される。
このような、真空に対する屈折率\(n_a\)のことを、物質\(a\)の絶対屈折率とよぶ。
物質\(a\)に対する物質\(b\)の相対屈折率\(n_{ab}\)は、\(n_{ab}=\frac{v_a}{v_b}\)であった。これを用いて相対屈折率を絶対屈折率で表すと、次のようになる。
この式(11)を、式(10)の相対屈折率に導入すると、
この式を変形させて、
スネルの法則はよくこの形で用いられる。
物質ごとに絶対屈折率は異なるが、これは物質ごとに波が通過する速度が異なるからである。等式\(λ=\frac{2πv}{ω}\)と、角振動数\(ω\)が屈折によって変化しないことより、波の速さ\(v\)が変わると波長\(λ\)も変化することがわかる。屈折前後で波長が変化するには、波は屈折するしかないため、波は屈折するのである。
まとめ
・反射の法則と屈折の法則(スネルの法則)を導出した。
参考文献
・長谷川修司(2009)『講談社基礎物理学シリーズ2 振動・波動』,講談社.

