エントロピー\(S\)とは、系の乱雑さ・不規則性を表す指標である。基準状態を\(O\)としたときの状態\(A\)におけるエントロピー\(S_A\)は、次のように定義される。
$$S(A)=\int_O^A \frac{d’Q}{T}$$
また、エントロピーを使えば、熱力学第一法則を次のように書き換えることができる。
$$dU=TdS-pdV$$
目次
カルノーサイクルによる任意のサイクルの分割
前提知識
可逆サイクル
前の記事で考えたカルノーサイクルは準静的過程が前提になっていたから、今回考えるサイクルは可逆サイクルであることに注意する。
参考:準静的過程
熱効率
前のカルノーサイクルの記事で、一般的な気体を使ったサイクルの効率\(η\)は、次のようになると触れた。
$$η=1-\frac{Q_2}{Q_1}$$
ただし、\(Q_1\)はサイクルに入ってくる熱量、\(Q_2\)はサイクルから出ていく熱量である。
さらに、理想気体のサイクルに限定すると、効率\(η\)は、温度\(T\)を使って次のようにも書ける。
$$η=1-\frac{T_2}{T_1}$$
ただし、\(T_1\)は等温過程で熱を吸収するときの温度、\(T_2\)は等温過程で熱を放出するときの温度を表す。
\(\frac{Q}{T}\)の和
2種類の熱効率の式を比較すると、次の関係が見える。
$$\frac{Q_2}{Q_1}=\frac{T_2}{T_1}$$
この式を次のように変形する。
$$\frac{Q_1}{T_1}=\frac{Q_2}{T_2}$$
左辺は高温熱源、右辺は低温熱源に関する量でまとめた。右辺を移項する。
$$\frac{Q_1}{T_1}+\frac{-Q_2}{T_2}=0$$
ここで、熱量\(Q\)の表し方を変える。\(Q\)を負の値もとれるようにして、気体が吸収する熱量を正、放出する熱量を負で表すことにする。そうすると、\(Q_2\)はサイクルが放出する熱量を表していたため、\(Q_2\)は負の値をとるようになる。これを考えて、上の式を書き換える。
$$\frac{Q_1}{T_1}+\frac{Q_2}{T_2}=0$$
カルノーサイクルによる任意のサイクルの分割
次に、任意の可逆サイクルについて考える。任意の可逆サイクルを\(n/2\)個のカルノーサイクルで分割すると、次の式を得る。
$$\displaystyle \sum_{ i = 1 }^{ n } \frac{Q_i}{T_i}=0$$
\(n \to ∞\)の極限をとると、任意の可逆サイクルを無限個で分割する場合を表すことができる。
$$\displaystyle \lim_{ n \to \infty } \sum_{ i = 1 }^{ n } \frac{Q_i}{T_i}=0$$
この式を積分で表すと、
$$\oint_{C’} \frac{d’Q}{T}=0$$
エントロピーの定義
\(\int_{A→B} \frac{d’Q}{T}\)は状態量か
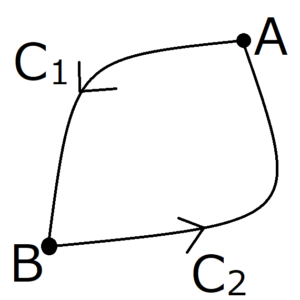
上の図のように、\(A\)と\(B\)を通るサイクルを考える。矢印に沿って\(A\)から\(B\)に進む経路を\(C_1\)、\(B\)から\(A\)に進む経路を\(C_2\)とする。そして経路\(C\)を、点\(A\)から矢印に沿って一周する経路と定義する。
$$C=C_1+C_2$$
任意の可逆過程のサイクルにおいて、\(\oint_{C’} \frac{d’Q}{T}=0\)だから、
経路\(C_2\)の逆向きの経路を\(C’_2\)とすると、\(\int_{C_2} \frac{d’Q}{T}=-\int_{C’_2} \frac{d’Q}{T}\)より、
$$\int_{C_1} \frac{d’Q}{T}=\int_{C’_2} \frac{d’Q}{T}$$
経路\(C_1\)と\(C’_2\)は任意にとることができたから、\(\int_A^B \frac{d’Q}{T}\)の値は始点と終点のみで決まり、経路に依存しない。
エントロピーの定義
基準状態\(O\)から状態\(P\)への経路を考える場合の\(S(P)\)を、次のように定義する。
$$S(P)=\int_O^P \frac{d’Q}{T}+S_0$$
これまでの議論より、\(S(P)\)は経路に依存せず、状態にのみ依存する状態量である。
エントロピーと熱力学第一法則
状態AからBまでの\(S\)は、次のように変形できる。
状態\(A\)と\(B\)が近いとして、\(S(B)-S(A)=dS\)とおくと、次の式が求まる。
$$d’Q=TdS$$
この式は可逆変化が前提となっていることに注意する。
これを使うと、熱力学第一法則は次のように書き換えられる。
$$dU=TdS-pdV$$
まとめ
・エントロピーの定義
$$S(P)=\int_O^P \frac{d’Q}{T}+S_0$$
・熱力学第一法則の書き換え
$$dU=TdS-pdV$$
参考文献
・藤井勝彦(1990)『統計力学』,マグロウヒル出版株式会社.
・三宅哲(1994)『熱力学』,裳華房.

