[mathjax]
クラウジウスの不等式
$$\oint \frac{d’Q}{T}≤0$$
この不等式は、可逆サイクルの熱効率が最大となることを利用すれば求められる。
クラウジウスの不等式の導出
前提知識
任意のサイクルの熱効率\(η’\)と可逆サイクルの熱効率\(η\)は、それぞれ次のようになる。
$$η’=1-\frac{Q_{out}}{Q_{in}}$$
$$η=1-\frac{T_{out}}{T_{in}}$$
$$(Q_{out}≤Q_{in},T_{out}≤T_{in})$$
そして両者の間には、次の式が成り立つ。
$$η’≤η$$
参考:カルノーサイクルの効率
2つのサイクルの熱効率の比較
上の前提知識の式を組み合わせると、次の式が求まる。
$$\frac{Q_{out}}{Q_{in}}≥\frac{T_{out}}{T_{in}}$$
\(Q_{out},\)\(Q_{in},\)\(T_{out},\)\(T_{in}\)は全部正だから、次のように書き換えられる。
$$\frac{Q_{in}}{T_{in}}-\frac{Q_{out}}{T_{out}}≤0$$
これまではサイクルに入る熱量\(Q_{in}\)も出ていく熱量\(Q_{out}\)もどちらも正で表してきた。ただしこれからは、熱量\(Q\)を負の値もとれるようにして、サイクルに入ってくる熱量を正、サイクルから出ていく熱量を負で表す。そうすると、左辺の第二項も正になる。
$$\frac{Q_{in}}{T_{in}}+\frac{Q_{out}}{T_{out}}≤0$$
n個の過程によるサイクル\(C\)の分割
上まではサイクルが、可逆過程と不可逆過程で合計2つの過程で成り立っている場合を考えた。では、サイクル\(C\)が、\(n\)個の過程で構成されている場合はどうなるだろうか。
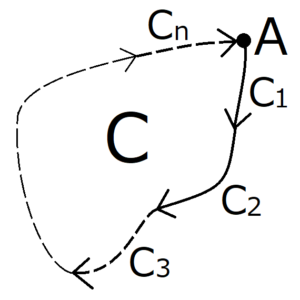
上図のように、任意のサイクル\(C\)が、合計\(n\)個の可逆・不可逆過程で構成されている。過程\(C_i\)において、温度\(T_i\)の熱源から熱\(Q_i\)を取り込んでいる。
前と同様に考えると、次の式が導ける。
$$\displaystyle \sum_{ i = 1 }^{ n } \frac{Q_i}{T_i}≤0$$
\(n \to \infty\)とすると、サイクル\(C\)を無限個の経路に分割できる。そして、この和は積分で表せるようになる。
$$\oint \frac{d’Q}{T}≤0$$
まとめ
可逆サイクルの熱効率が最大になることを利用して、クラウジウスの不等式が求められた。
参考文献
・三宅哲(1994)『熱力学』,裳華房.

