[mathjax]
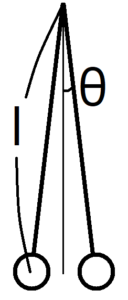
振れ角が十分小さい振り子運動は、単振動とみなすことができる。この記事では、運動方程式を組み立てることで、なぜ単振動とみなせるのか考える。
参考:単振動する物体の軌跡
目次
振り子の運動の表現方法
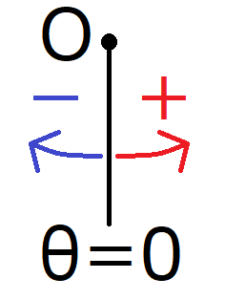
振り子の運動は、振り子の支点を原点とした極座標を使って表現される。支点の下方向を\(θ=0\)と定義して、そこから反時計回り方向の角度を正、時計回りの角度を負とする。
おもりにかかる力
張力と重力
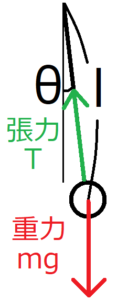
まず地球上のあらゆる物体には重力が働く。それに加えておもりにひもがつながっているため、そのひもからも力が加わっているはずである。このひもによる力を張力と呼ぶ。
極座標への変換
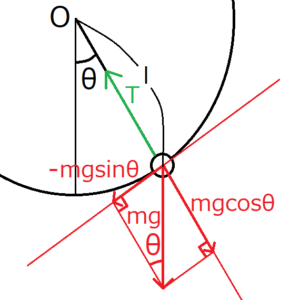
極座標で運動を考えるには、まずおもりに働く力を極座標に変換する必要がある。
動径方向の力
振り子のひもは伸縮しないと仮定すると、おもりは動径方向には動かない。したがって、動径方向の力はつりあっている。
$$mgcosθ=T$$
動径方向の運動方程式を考えても面白みはないので、これ以降は考えない。
角度方向の力
角度方向とは、上の図でいうと、半径\(l\)の円の接線方向のことを指す。
まず、張力は常に動径方向にかかっているから、張力の角度方向の成分は常に0である。次に、重力の角度方向の成分は、図より\(-mgsinθ\)になることがわかる。おもりが振れている方向とは逆方向に力がかかるため、マイナスをつけた。
以上より、おもりにかかる角度方向の力\(F_θ\)は、\(-mgsinθ\)である。
運動方程式の導出
おもりは常に半径\(l\)の円周上を動くことになるため、振り子の運動を考えるということは、角度方向の運動を考えることに他ならない。したがって、極座標で振り子の運動を考える場合、その運動方程式は角度\(θ\)についての方程式となる。
角度方向の運動方程式は、角度方向の力を\(F_θ\)、角度方向の速度を\(v_θ\)とすると、次の形をとる。
\(F_θ\)は前に求めたから、それを代入する。
\(v_θ\)を\(θ\)で表すには
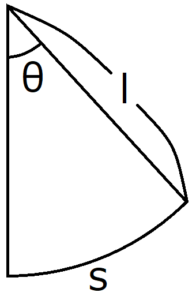
\(θ\)についての運動方程式を求めるには、\(v_θ\)を\(θ\)を使って表すことが不可欠だ。
扇形の弧の長さ\(s\)、中心角\(θ\)、半径\(l\)の間には次の関係がある。
$$s=lθ$$
半径\(l\)を定数として、両辺を時間\(t\)で微分する。
この式の左辺はおもりが半径\(l\)の円周上を進む速さ\(v_θ\)そのものだから、
これを式(1)に代入する。
両辺を\(ml\)で割る。
ここで、\(sinθ\)のマクローリン展開を考える。
\(θ\)が十分小さい場合、上の式の右辺の第二項以降は、第一項の\(θ\)と比べて十分小さくなると考えられる。したがって、この場合\(sinθ≒θ\)とみなせる。この関係を式(2)に導入すると、次の式を得る。
単振動の式との比較
ばねモデルの単振動の式は、次のように表された。
そして、\(\sqrt{\frac{k}{m}}\)は角振動数の次元を持っていたため、以降この値を\(ω\)とおく。
式(3)と式(4)を比較すると、同じ形の式となっていることがわかる。このことは、振り子の振れ角が十分小さいとき、その振り子の運動は単振動とみなせることを意味する。
参考:単振動する物体の軌跡
振り子の角振動数と周期
式(4)は単振動を表す式だから、この式(4)と、振り子の運動を表す式(3)を比較すれば、振り子の角振動数も求められる。
式(3)の中で、式(4)の角振動数\(ω^2\)に対応する部分は、\(\frac{g}{l}\)である。
また、周期は\(T=\frac{2π}{ω}\)で定義されたから、この定義に式(5)を代入すれば、振り子の周期も求まる。
これで、振り子の周期が求められた。この式から、振り子の周期はおもりの質量には依存せず、ひもの長さに依存することがわかる。
まとめ
・極座標を使って、振れ角が十分小さい場合の振り子の運動について考えた。
参考文献
・戸田盛和(1982)『力学〔物理入門コース1〕』,岩波書店.

