系の内部エネルギーの変化\(ΔU\)は、外部から系に入ってくる熱の総計\(Q\)と外部から系に加えられる仕事の総量\(W\)の和となる。これらの関係式を熱力学第一法則と呼ぶ。
$$ΔU=Q+W$$
また、本や教科書によっては、\(W\)を系が外部にする仕事と定義するものもある。この場合の熱力学第一法則は次のように定義される。
$$ΔU=Q-W$$
目次
熱力学第一法則の概要
熱・内部エネルギーとは
熱は19世紀までは質量の小さい物質だと考えられていたが、次第に熱はエネルギーと同一視でき、熱の移動はエネルギーの移動と同じであることが明らかになっていった。そして、物質を構成するあらゆる分子は絶えず振動しているという考えや、分子間のポテンシャルエネルギーによる分子間力から、熱は分子の力学的エネルギーであるという考えに発展した。ところが、熱は元々物質間で温度変化するときに、移動するものだと考えられていたため、最終的に、熱は高温部分から低温部分に移動する分子の力学的エネルギーと考えられるようになった。
内部エネルギーとは、系に含まれている分子の力学的エネルギーの総和のことを指す。
仕事\(W\)と熱力学第一法則
熱と内部エネルギーはどちらも力学的エネルギーだから、単位はジュール[J]となる。また、仕事の単位も当然ジュール[J]だから、力学的エネルギー保存則に沿って、これらを等式に並べることができる。それが熱力学第一法則である。
熱力学第一法則の2つの表し方
\(W\)を「系に加えられる仕事の総和」としたとき
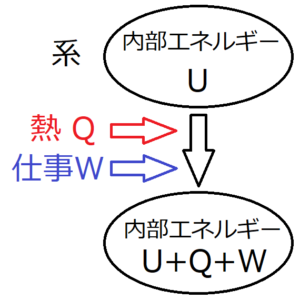
仕事が「系に加えられる仕事の総和」と定義されているため、仕事\(W\)が正ならば、その分内部エネルギーが増加することになる。したがって、入ってくる熱を\(Q\)とすると、次の式が成り立つ。
$$ΔU=Q+W$$
内部エネルギーの微小量をとると、次の式になる。
$$dU=d’Q+d’W$$
内部エネルギーの微小量\(dU\)は状態量だから、微小量は全微分となる。ところが熱\(Q\)と仕事\(W\)は経路によって変わるため、状態量でない。したがって、これらの微小量は全微分にはならない。だから、全微分と区別するために、\(Q\)や\(W\)の前に\(‘\)をつけた。
\(W\)を「系が外部にする仕事の総和」としたとき
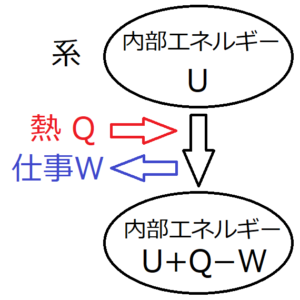
仕事が「系が外部にする仕事の総和」と定義されているため、仕事\(W\)が正ならば、その分内部エネルギーが減少することになる。したがって、入ってくる熱を\(Q\)とすると、次の式が成り立つ。
$$ΔU=Q-W$$
エントロピーを導入すると
エントロピー\(S\)という物理量を導入すると、熱力学第一法則は、次のように書き換えられる。
$$dU=TdS-pdV$$
詳しくは下の記事を参照してください。
参考:エントロピーの定義とは
まとめ
・熱とは、物体間で温度変化するときに移動する分子の力学的エネルギーを指す。
・内部エネルギーとは、系に含まれている分子の力学的エネルギーの総和を指す。
・仕事\(W\)が「系に加えられる仕事の総和」と定義されるときの熱力学第一法則は次の通りである。
$$ΔU=Q+W$$
また、この式の微小量をとると、次の式になる。
$$dU=d’Q+d’W$$
・仕事\(W\)が「系が外部にする仕事の総和」と定義されるときの熱力学第一法則は次の通りである。
$$ΔU=Q-W$$
参考文献
・都築嘉弘(2005)『チャート式シリーズ 新物理2』,数研出版.
・三宅哲(1994)『熱力学』,裳華房.


