[mathjax]
静磁場(時間変化しない磁場)\({\bf B}({\bf r})\)中を、\(Δ{\bf r}\)方向に流れる電流\(I\)にかかる力を、アンペールの力という。この力を\({\bf F}_B({\bf r})\)とおくと、次の式を満たす。
この式を使って、静電場と静磁場中の電荷が満たす運動方程式を導出する。
目次
単位体積あたりの力\({\bf f}_B\)
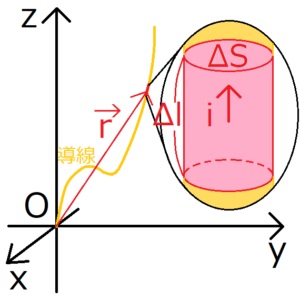
上図の導線に電流\(I\)が流れているとする。さらに、導線上の位置を点で表したものを\({\bf r}\)、\(Δ{\bf r}\)を位置\({\bf r}\)における微小部分を表すベクトルとする。底面積\(ΔS\)を通過する電流\(I\)と、電流密度\({\bf i}({\bf r})\)には、以下の関係が成り立つ。
一方、導線の単位体積当たりに働く力\({\bf f}_B({\bf r})\)を考える。微小円筒の体積は\(ΔSΔl\)だから、\({\bf F}_B({\bf r})\)と\({\bf f}_B({\bf r})\)の関係式は、
これらの式を上のアンペールの力の式に代入する。
電流密度\({\bf i}\)について
電流密度\({\bf i}({\bf r})\)を、電荷密度\(ρ({\bf r})\)と電荷の速度\({\bf v}\)で表すと、
これを上で求めた\({\bf f}_B\)の式に代入すると、
電荷\(e\)が位置\({\bf z}\)にあるときの電荷密度\(ρ\)をデルタ関数で表すと、\(ρ({\bf r})=eδ({\bf r}-{\bf z})\)になる。よって、
参考:デルタ関数と使用例
静磁場と静電場の影響
静電場\({\bf E}\)中の電荷密度\(ρ\)に働く力\({\bf f}_E\)は、次のように表せた。
したがって、静電場と静磁場の両方の影響を考えた力\({\bf f}={\bf f}_E+{\bf f}_B\)は、
\({\bf f}\)の体積積分
\({\bf f}\)は導線の単位体積当たりに働く力だったから、これを領域\(V\)で体積積分すると、領域\(V\)全体に働く力が求まる。ただし今回の場合、\({\bf f}\)はデルタ関数\(δ({\bf r}-{\bf z})\)を含んでいるため、電荷がある位置\({\bf z}\)にしか力は働かないことがわかる。
この電荷に働く力\(F\)をローレンツ力という。
運動方程式の構築
最後に、運動方程式\(m\dot{v}=F\)に上で求めた\(F\)を代入する。
これで、静電場と静磁場中の電子が従う運動方程式が求められた。
まとめ
静磁場中に存在する電流にかかるアンペールの力から、静電場と静磁場中の電子が従う運動方程式が求めた。
参考文献
・砂川重信(1987)『物理テキストシリーズ4 電磁気学』,岩波書店.

