[mathjax]
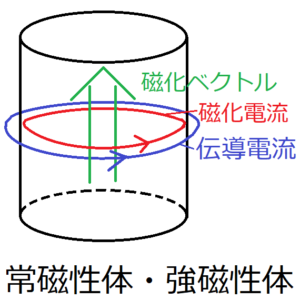
鉄芯が挿入されているコイルに電流を流すと、その鉄芯の表面に磁化電流が流れるようになる。この磁化電流による電流によって発生する磁場を、磁化ベクトルという。磁化ベクトルは、本によって\({\bf M}\)や\({\bf J}\)と表記される。厳密には、古典的には磁化ベクトルは発生しないが、量子力学導入までは暫定的にこのように磁化ベクトルを定義しておく。
目次
磁化ベクトル\(\bf M\)と磁気モーメント\(\bf m\)の違い
磁化ベクトルとは、単位体積あたりの磁気モーメントの平均のことである。数式で表すと、
式中の\(\displaystyle \sum_{ΔV} m_i\)はもちろん、\(ΔV\)内に存在する磁気モーメント全部の和を表す。
磁化を考慮したマクスウェル方程式の導出
アンペールの法則による磁束密度\(\bf B\)と磁化ベクトル\(\bf M\)の関係
アンペールの法則とは、マクスウェル方程式の1つであり、次の式のことを指した。
この式の両辺に透磁率\(μ_0\)をかけて変形する。
両辺を積分し、ストークスの定理を導入する。
ここで、磁束密度\({\bf B}\)は、電流\({\bf I}\)によるものだということに注意する。この電流\({\bf I}\)は、コイル内を流れている伝導電流\({\bf I}_e\)と、磁性体の表面を流れている磁化電流\({\bf I}_m\)の和になっている。だから、電流\({\bf I}\)によって発生する磁束密度\({\bf B}\)も、伝導電流による磁束密度\({\bf B}_e\)と磁化電流による磁束密度\({\bf B}_m\)で分解できる。磁化電流による磁場が磁化ベクトルだったから、これらは次のような関係を満たす。
この式の最初と最後の部分だけを取り出すと、
式(1)の両辺から\(\oint_C {\bf M} d{\bf r}=μ_0{\bf I}_m\)を引くと、
この式(2)は、磁性体の磁化を考慮した新しい形のマクスウェル方程式の積分形である。伝導電流\({\bf I}_e\)の電流密度を\({\bf j}_e\)とおくと、式(2)の微分形は次のようになる。
以上で、磁化を考慮したマクスウェル方程式が求められた。
磁場\(\bf H\)の定義
次のように磁場\(\bf H\)を定義する。
すると、式(2)は次のように書き換えられる。
また、磁場の定義の式を磁束密度で解いてみると、
ここで、コイルの中が真空である場合を考える。この場合当然磁化は存在しないから、\({\bf J}={\bf 0}\)である。
この\(μ_0\)を、真空中の透磁率とよぶ。
まとめ
・磁化ベクトルと磁気モーメントの違いを解説した
・磁化を考慮したマクスウェル方程式を求めた。
・磁化を考慮したマクスウェル方程式から、真空中の透磁率を考えた。
参考文献
・伊東敏雄(2008)『朝倉物理学選書2 電磁気学』,朝倉書店.
・砂川重信(1988)『電磁気学 ―初めて学ぶ人のために―』,培風館.

