身近な波動の例として、音波が挙げられる。音波とは、空気の振動によって伝わる波のことで、縦波である。前に弦の振動から波動方程式を求めることを別記事でしたが、こちらは縦波なので別に考える必要がある。
この記事では、なぜ縦波である音波も波動方程式に従うのかを考える。
力学
波束と分散について
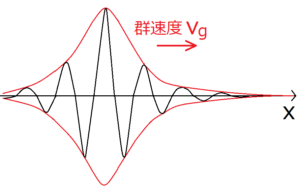
波束とは、限られた範囲にだけ存在する波のことをいう。高校までは主に全く同じ波形が無限に続くような波を考えてきたが、このような波は現実的でない。前の記事では波の重ね合わせによって生じるうなりによる群速度と位相速度について考えたが、それで学んだことは波束にも応用できる。
この記事では、古典力学の波動方程式に従う波束と、量子力学のシュレディンガー方程式に従う波束について考える。
参考:群速度と位相速度の導出
反射の法則とスネルの法則の導出
[mathjax]
反射の法則
$$θ_{in}=θ_r$$
屈折の法則(スネルの法則)
$$n_{in}sin{θ_{in}}=n_tsin{θ_t}$$
この記事では、平面波が上の2つの法則を満たすことを示す。
平面波と等位相面とは―波動方程式からsin波を導出する
[mathjax]
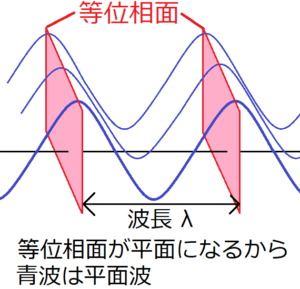
上の図では、同形の青い波が、奥にも複数存在する様子を表している。このような波では等位相面は平面になるため、図中の青い波は平面波と呼ばれる。
等位相面とは、同じ位相の場所を通り、かつ波の進行方向に対して垂直になるような面のことである。上の図では、波の頂上を通るような等位相面を赤い平面で表している。
この記事では、波動方程式から平面波を導出する。
コリオリの力とは
[mathjax]
コリオリの力とは、系\(S’\)が系\(S\)に対して回転運動をしているときに発生する見かけ上の力のことである。回転運動で発生する見かけ上の力としては遠心力が有名だが、コリオリの力と遠心力は全くの別物である。
この記事では、コリオリの力は数式でどう表されるのかを示す。
相対速度とガリレイ変換
[mathjax]
座標系\(S\)に対して、座標系\(S’\)が速度\(\bf V\)で等速平行移動している場合を考える。この場合、座標系\(S\)が慣性系ならば、座標系\(S’\)も慣性系となる。このことをガリレイの相対性原理という。この記事では、この原理の証明を行う。
ハミルトンの正準方程式
[mathjax]
正準方程式(ハミルトン方程式)
$$\dot{q}_i=\frac{∂H}{∂p_i}$$
$$\dot{p}_i=-\frac{∂H}{∂q_i}$$
正準方程式とは、上の2つの方程式のことである。この正準方程式の求め方は複数存在し、ハミルトニアンの全微分を使うものや、最小作用の原理を使うものなどがある。この記事では、ハミルトニアンの全微分を使う方法で、これらの正準方程式を導出する。
二体問題と換算質量
換算質量\(μ\)を導入することで、質量がそれぞれ\(m_1,m_2\)である2体の運動を、質量\(μ\)の1体の運動として考えることができる。この換算質量\(μ\)は、次の式を満たす。
$$\frac{1}{μ}=\frac{1}{m_1}+\frac{1}{m_2}$$
この記事では、重心周りの運動エネルギーから換算質量を求めてみる。
ハミルトニアンとは―定義と物理的意味について
[mathjax]
ハミルトニアン\(H\)とは、次のように定義される量のことである。
$$\displaystyle H(q,p,t)≡\sum_{i=1}^n p_i\dot{q}_i-L(q,\dot{q},t)$$
結論から言うと、ハミルトニアンは系の全エネルギーを表している。この記事では、なぜそう言えるのか確かめる。
振り子と単振動
[mathjax]
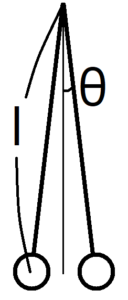
振れ角が十分小さい振り子運動は、単振動とみなすことができる。この記事では、運動方程式を組み立てることで、なぜ単振動とみなせるのか考える。
参考:単振動する物体の軌跡