固体物理の分野で結晶構造を考察するときは通常、結晶を格子とみなして考える。そしてその結晶格子の最小繰り返し単位のことを、単位格子とよぶ。単位格子は、頂点(格子点)・辺・面といった要素で構成されている。そしてそれらは、それぞれ結晶を構成する原子・原子間距離・格子点に囲まれた面(格子面)に対応している。
特に格子面は、結晶によるX線回折を考えるうえで不可欠な要素となっている。X線回折は結晶の同定に役に立つツールであるため、格子面への理解が重要であることは明らかだろう。
この記事では、結晶格子についてと、格子面の名前であるミラー指数について書く。
目次
単位格子について
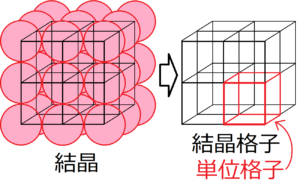
結晶を構成する原子の中心の位置のことを格子点というが、その格子点を、原子の結合に沿って線で結んだものを結晶格子という。
そして単位格子とは、結晶格子の最小繰り返し単位のことである。つまり、単位格子を隙間なく無限に並べたものが、結晶格子となる。
有名な例として、面心立方格子(fcc)、体心立方格子(bcc)、六方最密構造(hcp)が挙げられる。専門書ではカッコ内の略称がよく使われる。
ミラー指数とは
ここでは簡単のため、単位格子が立方晶である場合について考える。
結晶によるX線回折では、格子面によって反射されるX線を観測する。そのため、どの格子面によってX線が反射されたのかが重要である。したがって、格子面ごとに名前を決めておかなければならない。格子面を区別するための名前のことを、ミラー指数とよぶ。
X線解析をするといくつかのX線のピークが現れるのだが、このピークは特定の格子面が反射したX線を観測てきたことを意味する。観測できたX線のピークに、どの格子面の反射によるものなのかを記す作業のことを指数付けという。
ミラー指数は、(x,y,z)というように3つの数字の組として表記される。それぞれの数字はx,y,z軸の切片の座標の逆数に対応している。切片の座標ではなく、その逆数であることに注意。
ミラー指数の決め方
とある格子面のミラー指数は、その格子面を無限に延長させたときのx,y,z軸の切片の逆数で表せる。下に具体例を挙げる。
例題 (1,0,0)
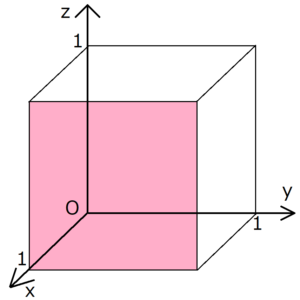
上の図の赤く塗られた格子面のミラー指数を考える。
まずx軸の切片は明らかにx=1である。ところがy,z軸に対しては平行であるため、決してこの格子面とy,z軸は交わらない。そこで、この格子面のy,z軸の切片は無限大であると考える。無限大の逆数を0とみなすと、格子面が軸に平行な場合は、その軸に対応するミラー指数は0になる。
したがって、それぞれの軸に交差する座標の逆数は、x,y,z軸それぞれ1,0,0となる。
以上より、求めるミラー指数は(1,0,0)となる。
平行な2つの線は、無限遠で交わるとみなせることを思い出そう。
例題 (2,0,0)
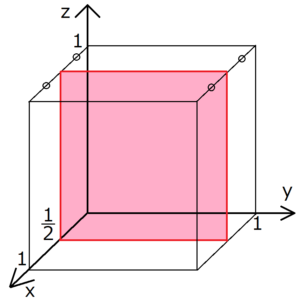
上の図の場合、x軸とはx=1/2で交わっている。y,z軸に関しては先ほどと同じである。
したがってそれぞれの座標の逆数は2,0,0となり、求めるミラー指数は(2,0,0)となる。
例題 (1,1/2,0)
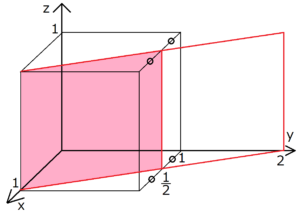
上の図の場合、x軸とはx=1で交わっているが、一見他の軸とは交わっていないように見える。ところが実際には、図のように格子面を延長させると、y=2でy軸と交わることがわかる。一方z軸とは、どれだけ格子面を延長させても決して交わらない。
したがって、求めるミラー指数は(1,1/2,0)となる。
マイナスを含むミラー指数の求め方
求めたいミラー指数が正だけの場合は単純に格子面を延長するだけでいいが、負の指数を含むとなると急にややこしく見える。だが、「結晶格子において平行な格子面は同一である」ことを意識すればそこまで難しくはない。
面 (0,-1,2)
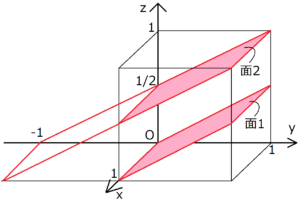
面1だけに注目すると、格子面のx軸の切片がわからない。それに加えてy,z軸の切片も0であるため、ミラー指数を求めようがない。
上の図では2つの面が書かれているが、実は結晶格子において平行な格子面は同一とみなすため、面1と面2は同じミラー指数で表示できる。つまり、面2のミラー指数だけを考えればよい。
面2を延長させると、y軸の切片はy=-1であることがわかる。それに、z軸の切片がz=1/2であることは、延長させなくても明らかだ。x軸には平行であるため、最終的なミラー指数は(0,-1,2)となる。
マイナスとなったミラー指数の値の書き方について、数字の上にバーを書いて\((0,\bar{1},2)\)と書くこともある。
まとめ
・ミラー指数は、基本的にはそれぞれの軸における格子面の切片の逆数として求まる。それで求められなかった場合、格子面を平行移動させることで求まる場合がある。
参考文献
・Charles Kittel(1998)『キッテル 固体物理学入門 第8版〈下〉』,宇野良清・津屋昇・森田章・山下次郎訳, 丸善株式会社.

