経験事実より、次の原理が提唱された。
トムソンの原理
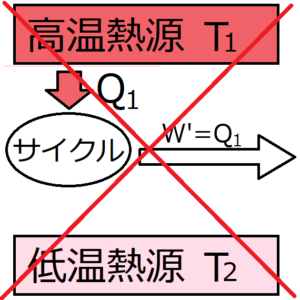
他に変化を残さずに、一つの熱源から熱を取り込んで、その熱をすべて仕事に変換するサイクルは存在しない。
クラウジウスの原理
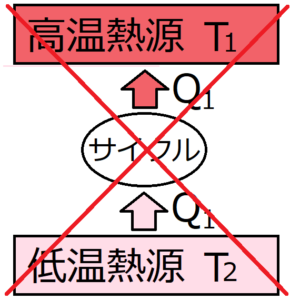
他に変化を残さずに、熱を低熱源から高熱源へ移動させるようなサイクルは存在しない。
「他に変化を残さずに」とは具体的には、サイクルが外部に対して仕事をしたり、高熱源や低熱源に対して熱を放出・吸収したりしないことを指す。
ビオ・サバールの法則
ビオ・サバールの法則
ビオ・サバールの法則とは、位置\({\bf r}\)における、電流による磁束密度\({\bf B}\)を表す式である。この式はビオとサバールによって行われた実験によって求められたものである。
$$d{\bf B}=\frac{μ_0}{4π}･\frac{Id{\bf s}×{\bf r}}{r^3}$$
\(d{\bf s}\):電流が進む向きを表すベクトル \(I\):電流の強さ
位置\({\bf r}\)における磁束密度\({\bf B}\)を求めるには、上の式の両辺を積分すればよい。この式の右辺に含まれている微小量は\(d{\bf s}\)であるため、電流の通り道に沿って積分する。
古典的・量子力学的に考える磁化
[mathjax]
量子力学が提唱されるはるか昔に、アンペールは、古典的な視点から磁化を説明した。それによると、磁化は分子電流によって発生するものとされている。ところが量子力学誕生後、磁化は電子のスピン(自転)などによるものであることが分かってきた。この記事では、磁化を古典的・量子的の両方の視点から見てみる。
静電場と静磁場中の電荷の運動方程式
[mathjax]
静磁場(時間変化しない磁場)\({\bf B}({\bf r})\)中を、\(Δ{\bf r}\)方向に流れる電流\(I\)にかかる力を、アンペールの力という。この力を\({\bf F}_B({\bf r})\)とおくと、次の式を満たす。
$${\bf F}_B({\bf r})=IΔ{\bf r}×{\bf B}({\bf r})$$
この式を使って、静電場と静磁場中の電荷が満たす運動方程式を導出する。
デルタ関数と使用例
[mathjax]
デルタ関数\(δ(x-a)\)とは、カッコの中が\(0\)のときのみ特殊な値になるようなものであり、次のようにして定義される。
$$\int_{-∞}^∞ f(x)δ(x-a)dx=f(a)$$
このデルタ関数は名前に関数とついているが、正確には関数ではない。そのため、このように積分を使って定義される。
波動方程式を弦の振動から導出してみた
通常、連続的な物体の運動を考えるときは、その物体を細かく分解して考える。今回考える弦の振動も例外ではない。
今回は、弦の運動が一次元の波動方程式を満たすことを示す。
内積・外積の用途
\({\bf A}=(a_x,a_y,a_z)\)、\({\bf B}=(b_x,b_y,b_z)\)
内積
\begin{eqnarray} {\bf A}･{\bf B}&=&a_xb_x+a_yb_y+a_zb_z\\&=&|{\bf A}||{\bf B}|cosθ \end{eqnarray}
外積
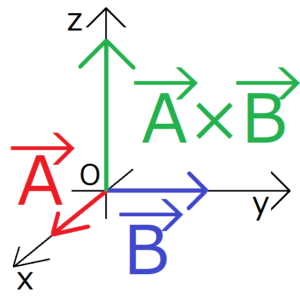
右ねじを意識すれば外積の向きを間違えない。
\begin{eqnarray} {\bf A}×{\bf B}&=&\begin{vmatrix} {\bf i}&{\bf j}&{\bf k}\\a_x&a_y&a_z\\b_x&b_y&b_z \end{vmatrix}\\&=&{\bf i}(a_yb_z-a_zb_y)+{\bf j}(a_zb_x-a_xb_z)+{\bf k}(a_xb_y-a_yb_x) \end{eqnarray}
$$|{\bf A}×{\bf B}|=|{\bf A}||{\bf B}|sinθ$$
参考:行列式の計算方法
ローレンツゲージとは
ゲージ変換を導入すれば、電磁ポテンシャルが満たす式を次のようにきれいな形に変形できる。
$$\left( ∇^2-\frac{1}{c^2}\frac{∂^2}{∂t^2} \right){\bf A}(t,{\bf r})=-μ_0{\bf j}(t,{\bf r})$$
$$\left( ∇^2-\frac{1}{c^2}\frac{∂^2}{∂t^2} \right)φ=-\frac{1}{ε_0}ρ$$
ポインティングベクトルの意味と絶対値
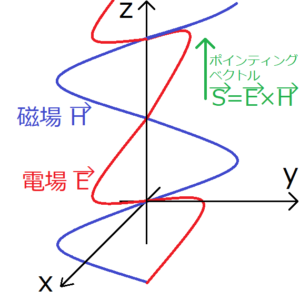
ポインティングベクトル\({\bf S}(t,{\bf r})\)とは、電磁場の流れを表すものであり、次のように定義される。
$${\bf S}({\bf r},t)={\bf E}({\bf r},t)×{\bf H}({\bf r},t)$$
熱力学におけるマクスウェルの関係式
内部エネルギー、ヘルムホルツの自由エネルギー、エンタルピー、ギブスの自由エネルギーは、それぞれ次のように定義される。
内部エネルギー \(U\)
$$U=d’Q-d’W’$$
ヘルムホルツの自由エネルギー\(F\)
等温変化において、内部エネルギー\(U\)の中で仕事として取り出せるエネルギー。
$$F=U-TS$$
エンタルピー\(H\)
エンタルピーは次のように定義され、エネルギーの次元をもつ。\(U,p,V\)のすべてが状態量だから、エンタルピーも状態量である。
$$H=U+pV$$
参考:エンタルピーとは
ギブスの自由エネルギー\(G\)
エンタルピー\(H\)から\(TS\)を引いたもの。
$$G=U+pV-TS$$