ギブスの自由エネルギー\(G\)とは、次のように定義される量のことである。
このギブスの自由エネルギー\(G\)は、定圧過程における熱量(エンタルピー)\(H\)を含んでいる。
この記事では、ギブスの自由エネルギーを使って、相転移現象について考える。この記事を読み進める前に、少なくとも下の2つの記事を先に読んでおくことをおすすめする。
参考:エンタルピーとは
目次
なぜギブスの自由エネルギーで考えるのか
相転移について考えるときは、ギブスの自由エネルギーを使う場合が多い。その理由は、普段私たちが実験する環境は、定圧であることが多いからだ。例えば、常温で氷を水に状態変化させる実験を行ったとする。この場合、真空ポンプなどの何か特殊な装置を使わない限り、大気圧下で実験をすることになる。
自由エネルギーには他にヘルムホルツの自由エネルギー\(F\)があるが、こちらは定積環境における熱量となる内部エネルギー\(U\)を含む。ところが、氷は水に変化するときに体積が変化するため、この相転移をヘルムホルツの自由エネルギーで考えるのはよくない。つまり、定積変化は身近ではないのである。
要するに定圧環境のほうが私たちにとって身近だから、ギブスの自由エネルギーがよく使われるのだ。もちろんヘルムホルツの自由エネルギーのほうを使うこともあるのだが、最終的にどちらを使うかは、今自分が行っている実験から、適切なほうを自分で選ばなくてはならない。ただし今回はより一般的なギブスの自由エネルギーを使う。
A相とB相間の相転移
共存曲線上の化学ポテンシャル
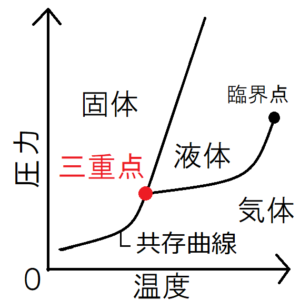
物質の状態は、圧力と温度で決まる。物質の状態をp-Tグラフ上で表した図を、相図という。上の図はその一例である。相図中の2つの状態を隔てている黒線は、2つの状態が共存している状態を表すため、共存曲線とよばれる。
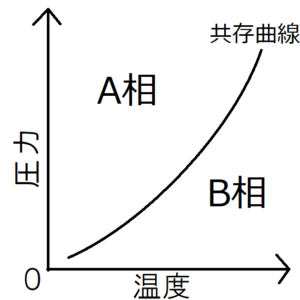
ここで、ギブスの自由エネルギー\(G\)における化学ポテンシャル\(μ\)は、圧力\(p\)と温度\(T\)のみに依存する関数であったことを思い出す。だから、A相とB相の両方に含まれる共存曲線上では、A相の化学ポテンシャル\(μ_A\)とB相の化学ポテンシャル\(μ_B\)は等しくなる。
参考:化学ポテンシャルとは
相転移によるギブスの自由エネルギーの変化
A相とB相が共存している系を考える。A相、B相を構成している分子(または原子)の物質量を、それぞれ\(N_A,N_B\)とおく。さらに、それぞれの相のギブスの自由エネルギーを\(G_A,G_B\)とおくと、系全体のギブスの自由エネルギー\(G\)は次のようになる。
ここで、B相からA相への相転移を考える。物質量\(δN_A\)だけ相転移が完了したとすると、上の式の変数は次のように書き換えられる。
物質量\(δN_A\)の相転移による全体のギブスの自由エネルギーの変化は、
共存曲線上ではない場合、\(μ_A≠μ_B\)である。
相転移の向きについて
\(δN_A\)はB相からA相へ転移する分子の物理量を表していたから、\(δN_A\)の符号の取り方を考えることが、相転移の向きを考えることにもつながる。
ギブスの自由エネルギーが減少方向に反応が進むように\(δN_A\)の符号をとりたい。そのためには式(1)より、\(δN_A\)の符号は、\((μ_A-μ_B)\)とは逆向きと定義すればよいことがわかる。具体的には、「\(μ_A-μ_B>0\)ならば\(δN_A<0\)」、「\(μ_A-μ_B<0\)ならば\(δN_A>0\)」と定義する。
まず、「\(μ_A-μ_B>0\)ならば\(δN_A<0\)」の場合を考える。化学ポテンシャルの式の片方の項を移項させると、「\((μ_A>μ_B)\)ならば\(δN_A<0\)」と言い換えができる。そして、\(δN_A\)が負であることは、A相からB相への移動した物質量を意味する。このことと「\(μ_A>μ_B\)」という仮定をあわせて考えると、化学ポテンシャル\(μ\)が小さい方向に相転移が進むことがわかる。
「\((μ_A-μ_B)<0\)ならば\(δN_A>0\)」の場合でも、先ほどと同様に考えることで、化学ポテンシャルが小さい相に相転移することがいえる。
まとめ
・相転移は、化学ポテンシャルが小さい相に向かう。
参考文献
・三宅哲(1994)『熱力学』,裳華房.

