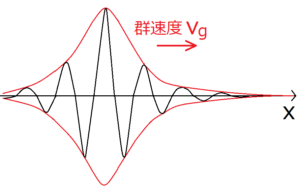
波束とは、限られた範囲にだけ存在する波のことをいう。高校までは主に全く同じ波形が無限に続くような波を考えてきたが、このような波は現実的でない。前の記事では波の重ね合わせによって生じるうなりによる群速度と位相速度について考えたが、それで学んだことは波束にも応用できる。
この記事では、古典力学の波動方程式に従う波束と、量子力学のシュレディンガー方程式に従う波束について考える。
参考:群速度と位相速度の導出
目次
群速度と位相速度の定義
群速度\(v_g\)と位相速度\(v_φ\)は、次のように定義された。
それぞれを簡単に解説する。群速度は波束の速度のことである。もう少し厳密に言うと、波束の中心(波束の最も振幅が大きい場所)の速度のことを群速度という。前の記事ではうなりの速度のことを群速度と呼んだが、それと似ていることがわかるだろう。一方の位相速度とは、波束の中に含まれる細かい波の速度のことを指す。
群速度と位相速度の大小と波束の時間変化の関係
群速度と位相速度の大小に注目すると、波束が時間経過につれてどのように変化していくのかがわかる。ここでは、それぞれの場合における波束の時間変化について考える。
位相速度=群速度の場合
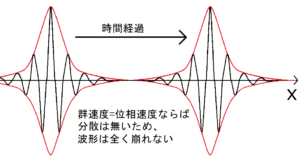
群速度と位相速度が等しい場合、波形が完全に維持された状態で平行移動するような波が観測される。波束の速度とその中身の速度が同じなのだから、このことは直感的にも理解しやすいだろう。このような条件を満たす波束は、時間経過で広がっていくことはない。
具体例
群速度と位相速度が等しい波束の具体例は、波動方程式の解が挙げられる。事実、波動方程式
の解
の分散関係は、次のようになった。
$$ω^2=v^2k^2$$
この式は、角振動数\(ω\)と波数\(k\)が比例関係にあることを意味している。
参考:平面波と等位相面とは―波動方程式からsin波を導出する
そしてこの比例関係は、位相速度と群速度が等しいことを表している。
なぜ比例関係から分散が無いといえるのか
$$ω=vk$$
以上より、
群速度と位相速度が等しいことになるため、角振動数と波数が比例関係である場合は分散が無いといえる。
波動方程式に従う波は分散がない
波動方程式に従う波の具体例として、弦を伝わる波や空気中を伝わる音波などが挙げられる。このような波は、周波数によって波の速度が変わるということはない。事実、弦を伝わる波の速度は弦の張力と線密度のみに依存していて、周波数に依らなかった。さらに、日常生活でも音の高さ(音の周波数)によって音速が異なるということがないことも明らかだろう。
位相速度≠群速度の場合
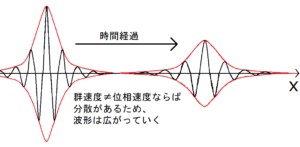
位相速度と群速度が異なる場合は、波が時間経過で進むに連れて広がっていく。このことを分散があるという。
具体例
位相速度と群速度が異なる波束の具体例は、シュレディンガー方程式の解が挙げられる。事実、シュレディンガー方程式
の解の分散関係は、
となる(波を表す式\(Ψ(x,t)=Ae^{i(kx-ωt)}\)を代入すれば求まる)。これをもとに群速度と位相速度を求める。
このように、シュレディンガー方程式に従う波束の群速度と位相速度は異なる。そのため、シュレディンガー方程式に従う波束は分散があるといえる。
ちなみに、この波束の波動関数\(Ψ(t,x)\)の絶対値の2乗\(|Ψ(t,x)|^2\)は、粒子の存在確率を表している。そして、粒子の存在確率に分散があるということは、電子のような素粒子は時間経過につれて存在しうる場所が広がっていくということになる。ちなみに最小の分散は\(ℏ/2\)になり、この事実は量子力学の不確定性原理につながっていくことになる。このことについては後日記事にする予定である。
まとめ
・波束とは、限られた範囲にだけ存在する波のことを指す。
・群速度と位相速度が等しければ分散がないが、異なる場合は分散がある。
・分散があると、波束は時間経過でつぶれてしまう。
・分散の有無は、分散関係の式を見れば分かる。角振動数ωと波数kが比例関係であれば、分散がない。
参考文献
・長谷川修司(2009)『講談社基礎物理学シリーズ2 振動・波動』,講談社.
・原田勲・杉山忠男(2011)『講談社基礎物理学シリーズ6 量子力学I』,講談社.


