[mathjax]
エネルギー保存則とは運動エネルギー\(T\)とポテンシャルエネルギー\(V\)の和が一定になるというものであった。この記事では、ラグランジアンを使って、解析力学的にこの法則を証明する。
この記事を読む前に、下の記事を読んでおくことを強くおすすめする。ラグランジアンやラグランジュ方程式の導出が載っている。
力学
ラグランジュ運動方程式の導出
[mathjax]
ラグランジアン\(L\)の定義
$$L≡T-V$$
ラグランジュ方程式
i番目の粒子の位置\(q_i\)と速度\(\dot{q}_i\)を使ったラグランジュ方程式
$$\frac{d}{dt}\left(\frac{∂L}{∂\dot{q}_i}\right)-\frac{∂L}{∂q_i}=0$$
この記事ではこれらの式を導出する。
剛体の運動方程式
[mathjax]
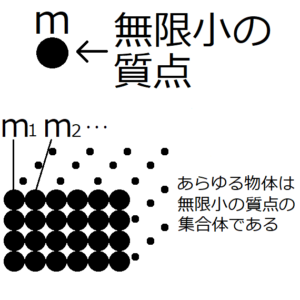
力を加えても変形しない物体を剛体という。そして、剛体は質点の集合体とみなすことができる。この記事では、剛体の運動方程式を導出してみる。
$$\displaystyle M\frac{d^2{\bf r}_G}{dt^2}=\sum_{i=1}^N {\bf F}_i$$
天秤から考える重心の意味と導出
[mathjax]
重心
$$ {\bf r}_G=\frac{\displaystyle \sum_{i=1}^N m_i{\bf r}_i}{\displaystyle \sum_{i=1}^N m_i }$$
力積と運動量の関係
力積とは、時間\(Δt\)の間に、力\({\bf F}\)が物体に与える運動量のことである。数式では、次の式の左辺のような形をとる。
$${\bf F}･Δt={\bf p}(t_0+Δt)-{\bf p}(t_0)･･･(1)$$
この記事では、まず力積のイメージをF-tグラフでつけた後、壁がボールに与える力積を求める。
ニュートンの運動の法則と質量の意味
[mathjax]
ニュートンの運動の第1法則(慣性の法則)
物体に働く力がつり合っていたり、全く力が働いていない場合、その物体は静止し続けるか、等速直線運動をする。
ニュートンの運動の第2法則(運動方程式)
力\({\bf F}\)、物体の質量\(m\)、物体の位置\({\bf r}(t)\)は次の関係を満たす。
$${\bf F}=m\frac{d^2{\bf r}(t)}{dt^2}$$
ニュートンの運動の第3法則(作用反作用の法則)
物体Aが物体Bに力を与えるとき、物体Bも物体Aに対して、その力と同じ大きさかつ逆向きの力を与える。
仮想仕事とダランベールの原理
[mathjax]
仮想仕事の原理
$$\displaystyle \sum_i {\bf F}_i･δ{\bf r}_i=0$$
ダランベールの原理
$$\displaystyle \sum_{ i } ({\bf F}_i-\dot{\bf p}_i)･δ{\bf r}_i=0$$
波動方程式を弦の振動から導出してみた
通常、連続的な物体の運動を考えるときは、その物体を細かく分解して考える。今回考える弦の振動も例外ではない。
今回は、弦の運動が一次元の波動方程式を満たすことを示す。
群速度と位相速度の導出
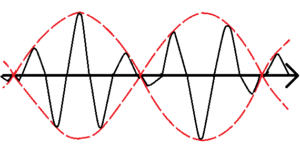
上図は、2種類の波が重なり合ってうなりが発生している様子を表している。波の振幅を赤い点線で結んだが、群速度\(v_g\)とは、この赤線で表した波が動く速度を表したものである。このことから、群速度はうなりの構造の速度とよく言われる。
$$v_g≡\frac{dω}{dk}$$
一方、黒い実線の波の速さは位相速度\(v_φ\)と呼ぶ。
$$v_φ≡\frac{\bar{ω}}{\bar{k}}$$
力のモーメントと角運動量の関係
従来の運動量\({\bf p}=m{\bf v}\)は、物体の並進運動の勢いや激しさを表していた。これの回転運動バージョンが角運動量である。つまり角運動量\({\bf L}\)とは、回転軸に対する回転運動の勢いや激しさを表すパラメータである。
$${\bf L} \equiv {\bf r}×{\bf p}$$
力のモーメント\({\bf N}\)とは、回転軸に対して物体を回転させようとする力の大きさを表す。トルクと呼ばれることもある。
$${\bf N} \equiv {\bf r}×{\bf F}$$
角運動量ベクトル\({\bf L}\)と力のモーメントのベクトル\({\bf N}\)の関係は次の通りになる。
$$\frac{d{\bf L}}{dt}={\bf N}$$
この記事では、２次元平面と３次元空間でこの\({\bf L}\)と\({\bf N}\)の関係式が成り立つことを示す。