熱力学

経験事実より、次の原理が提唱された。

トムソンの原理

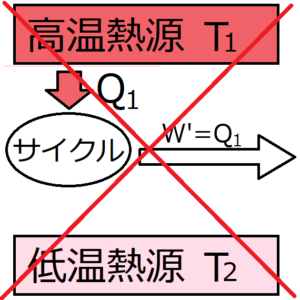
他に変化を残さずに、一つの熱源から熱を取り込んで、その熱をすべて仕事に変換するサイクルは存在しない。

クラウジウスの原理

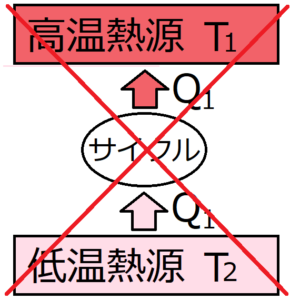
他に変化を残さずに、熱を低熱源から高熱源へ移動させるようなサイクルは存在しない。

「他に変化を残さずに」とは具体的には、サイクルが外部に対して仕事をしたり、高熱源や低熱源に対して熱を放出・吸収したりしないことを指す。

続きを読む

内部エネルギー、ヘルムホルツの自由エネルギー、エンタルピー、ギブスの自由エネルギーは、それぞれ次のように定義される。

内部エネルギー \(U\)

$$U=d’Q-d’W’$$

ヘルムホルツの自由エネルギー\(F\)

等温変化において、内部エネルギー\(U\)の中で仕事として取り出せるエネルギー。

$$F=U-TS$$

エンタルピー\(H\)

エンタルピーは次のように定義され、エネルギーの次元をもつ。\(U,p,V\)のすべてが状態量だから、エンタルピーも状態量である。

$$H=U+pV$$

参考:エンタルピーとは

ギブスの自由エネルギー\(G\)

エンタルピー\(H\)から\(TS\)を引いたもの。

$$G=U+pV-TS$$

続きを読む

エントロピー\(S\)とは、系の乱雑さ・不規則性を表す指標である。基準状態を\(O\)としたときの状態\(A\)におけるエントロピー\(S_A\)は、次のように定義される。

$$S(A)=\int_O^A \frac{d’Q}{T}$$

また、エントロピーを使えば、熱力学第一法則を次のように書き換えることができる。

$$dU=TdS-pdV$$

続きを読む

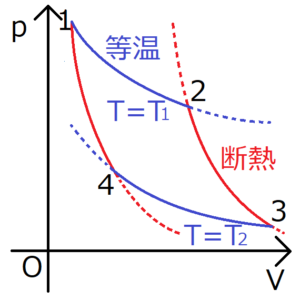
カルノーサイクルとは、等温過程と断熱過程という2種類の準静的過程で構成された熱機関のことである。

この記事では、このサイクルにおける仕事と熱効率の導出を行う。

続きを読む

系がした仕事を\(W’\)とおく。系Aがそれぞれの過程を経て系Bに至ったとき、次の式が成り立つ。

・定圧過程

一般的な気体:\(W’_{A→B}=p(V_B-V_A)\)

理想気体:\(W’_{A→B}=nR(T_B-T_A)\)

・等温過程

理想気体:\(W’_{A→B}=nRTln\frac{V_B}{V_A}\)

・断熱自由膨張

理想気体:\( \left( \frac{∂U}{∂V} \right) _T=0\)(ジュールの法則)

理想気体:\(C_p-C_V=nR\)(マイヤーの法則)

理想気体:\(dU=C_VdT\)

・断熱過程

理想気体:\(TV^{γ-1}=(定数)\)

理想気体:\(pV^γ=(定数)\)

続きを読む

温度\(T\)が一定のときに圧力\(p\)と体積\(V\)が反比例することをボイルの法則、圧力\(p\)が一定のときに体積\(V\)は温度\(T\)に比例することをシャルルの法則という。これらを1つの式で表したものをボイル-シャルルの法則と呼ぶ。

$$\frac{pV}{T}=C(一定)$$

理想気体とは、ボイル・シャルルの法則に正確に従うような気体のことである。理想気体の状態方程式とは次の式のことを指す。

$$pV=nRT$$

続きを読む

圧縮率\(κ\)

等温圧縮率\(κ_T\)

体積弾性率\(k_T\)

体膨張率\(α\)

続きを読む

熱容量とは、準静的に熱量を加える場合で、物体の温度を1K(ケルビン)上げるのに必要な熱量のことである。数式で表すと次のようになる。

また、定積熱容量\(C_V\)と定圧熱容量\(C_p\)は、それぞれ

この記事では、上の2式を導出する。

続きを読む

準静的過程とは、系に膨張・圧縮・加熱・冷却といった変化がゆっくり行われることで、常に平衡状態を保ちながら変化するような過程のことである。準静的過程によって変化した系は、その過程を逆向きにたどれば、再び元の状態に戻れるという特徴をもつ。

続きを読む

系の内部エネルギーの変化\(ΔU\)は、外部から系に入ってくる熱の総計\(Q\)と外部から系に加えられる仕事の総量\(W\)の和となる。これらの関係式を熱力学第一法則と呼ぶ。

$$ΔU=Q+W$$

また、本や教科書によっては、\(W\)を系が外部にする仕事と定義するものもある。この場合の熱力学第一法則は次のように定義される。

$$ΔU=Q-W$$

続きを読む