[mathjax]
電荷には、電場を発生させる能力がある。そして、重力ポテンシャルと同様にして、電場によるポテンシャルも考えることができる。このポテンシャルのことを電位と呼ぶ。
この記事では、電位をポテンシャルエネルギーの式から求めてみる。
電場をクーロン力の式から定義する
[mathjax]
前の記事では電荷とは何かを考えたが、この電荷は、周囲の空間に影響を及ぼすことができる。このような周囲の空間への影響のことを一般的に場とよぶのだが、特に電荷がつくる場のことを電場という。
この記事では、一つの電荷が作り出す電場について考える。
参考:電荷とクーロンの法則
潜熱と相転移
潜熱とは、相Aから相Bに相転移するときに、系に出入りする熱のことである。この記事では、なぜ相転移に潜熱がつきものなのかを考える。
ギブスの自由エネルギーと相転移の向き
ギブスの自由エネルギー\(G\)とは、次のように定義される量のことである。
$$G≡H-TS$$
このギブスの自由エネルギー\(G\)は、定圧過程における熱量(エンタルピー)\(H\)を含んでいる。
この記事では、ギブスの自由エネルギーを使って、相転移現象について考える。この記事を読み進める前に、少なくとも下の2つの記事を先に読んでおくことをおすすめする。
参考:エンタルピーとは
反射の法則とスネルの法則の導出
[mathjax]
反射の法則
$$θ_{in}=θ_r$$
屈折の法則(スネルの法則)
$$n_{in}sin{θ_{in}}=n_tsin{θ_t}$$
この記事では、平面波が上の2つの法則を満たすことを示す。
平面波と等位相面とは―波動方程式からsin波を導出する
[mathjax]
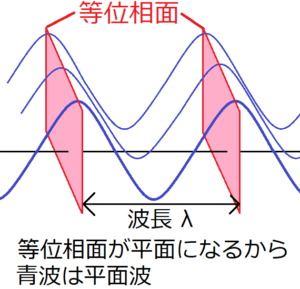
上の図では、同形の青い波が、奥にも複数存在する様子を表している。このような波では等位相面は平面になるため、図中の青い波は平面波と呼ばれる。
等位相面とは、同じ位相の場所を通り、かつ波の進行方向に対して垂直になるような面のことである。上の図では、波の頂上を通るような等位相面を赤い平面で表している。
この記事では、波動方程式から平面波を導出する。
コリオリの力とは
[mathjax]
コリオリの力とは、系\(S’\)が系\(S\)に対して回転運動をしているときに発生する見かけ上の力のことである。回転運動で発生する見かけ上の力としては遠心力が有名だが、コリオリの力と遠心力は全くの別物である。
この記事では、コリオリの力は数式でどう表されるのかを示す。
相対速度とガリレイ変換
[mathjax]
座標系\(S\)に対して、座標系\(S’\)が速度\(\bf V\)で等速平行移動している場合を考える。この場合、座標系\(S\)が慣性系ならば、座標系\(S’\)も慣性系となる。このことをガリレイの相対性原理という。この記事では、この原理の証明を行う。
ハミルトンの正準方程式
[mathjax]
正準方程式(ハミルトン方程式)
$$\dot{q}_i=\frac{∂H}{∂p_i}$$
$$\dot{p}_i=-\frac{∂H}{∂q_i}$$
正準方程式とは、上の2つの方程式のことである。この正準方程式の求め方は複数存在し、ハミルトニアンの全微分を使うものや、最小作用の原理を使うものなどがある。この記事では、ハミルトニアンの全微分を使う方法で、これらの正準方程式を導出する。
二体問題と換算質量
換算質量\(μ\)を導入することで、質量がそれぞれ\(m_1,m_2\)である2体の運動を、質量\(μ\)の1体の運動として考えることができる。この換算質量\(μ\)は、次の式を満たす。
$$\frac{1}{μ}=\frac{1}{m_1}+\frac{1}{m_2}$$
この記事では、重心周りの運動エネルギーから換算質量を求めてみる。