[mathjax]
ハミルトニアン\(H\)とは、次のように定義される量のことである。
$$\displaystyle H(q,p,t)≡\sum_{i=1}^n p_i\dot{q}_i-L(q,\dot{q},t)$$
結論から言うと、ハミルトニアンは系の全エネルギーを表している。この記事では、なぜそう言えるのか確かめる。
振り子と単振動
[mathjax]
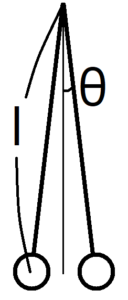
振れ角が十分小さい振り子運動は、単振動とみなすことができる。この記事では、運動方程式を組み立てることで、なぜ単振動とみなせるのか考える。
参考:単振動する物体の軌跡
解析力学によるエネルギー保存則の導出
[mathjax]
エネルギー保存則とは運動エネルギー\(T\)とポテンシャルエネルギー\(V\)の和が一定になるというものであった。この記事では、ラグランジアンを使って、解析力学的にこの法則を証明する。
この記事を読む前に、下の記事を読んでおくことを強くおすすめする。ラグランジアンやラグランジュ方程式の導出が載っている。
ラグランジュ運動方程式の導出
[mathjax]
ラグランジアン\(L\)の定義
$$L≡T-V$$
ラグランジュ方程式
i番目の粒子の位置\(q_i\)と速度\(\dot{q}_i\)を使ったラグランジュ方程式
$$\frac{d}{dt}\left(\frac{∂L}{∂\dot{q}_i}\right)-\frac{∂L}{∂q_i}=0$$
この記事ではこれらの式を導出する。
誘電体と分極
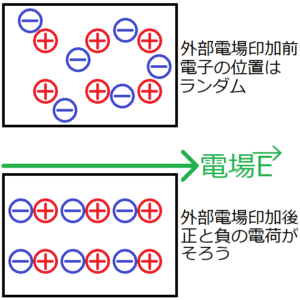
誘電体とは、外部電場をかけたときに分極するような物体のことである。誘電体は電気を通さないため、不導体とも呼ばれる。コンデンサーの間に挿入すると、電気容量が大きくなる。
この記事では、電束密度と分極ベクトルの定義を確認した後、公式\({\bf D}=ε{\bf E}\)を導出する。
電荷とクーロンの法則
[mathjax]
髪の毛に下敷きをこすって逆立てる遊びを小さいころにした人は多いだろう。この現象が起こる理由は、片方の物体に含まれている電荷がもう片方に移動することで、それぞれの物体が違う種類の電荷によって帯電するからである。
磁化率と残留磁化
[mathjax]
外部磁場が0のときに磁化ベクトルも0になる等方的な物質において、外部磁場が小さいとき、磁化ベクトル\(\bf M\)は外部磁場\({\bf H}_{ex}\)に比例する。この比例定数を磁化率\(χ_m\)という。
$${\bf M}=χ_m{\bf H}_{ex}･･･(1)$$
この磁化率が正の場合は常磁性体か強磁性体、負の場合は反磁性体を表す。
磁化を考慮したマクスウェル方程式の導出
[mathjax]
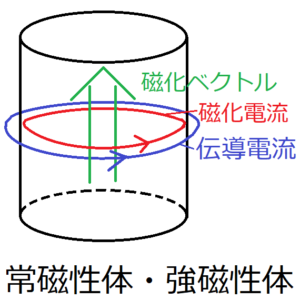
鉄芯が挿入されているコイルに電流を流すと、その鉄芯の表面に磁化電流が流れるようになる。この磁化電流による電流によって発生する磁場を、磁化ベクトルという。磁化ベクトルは、本によって\({\bf M}\)や\({\bf J}\)と表記される。厳密には、古典的には磁化ベクトルは発生しないが、量子力学導入までは暫定的にこのように磁化ベクトルを定義しておく。
剛体の運動方程式
[mathjax]
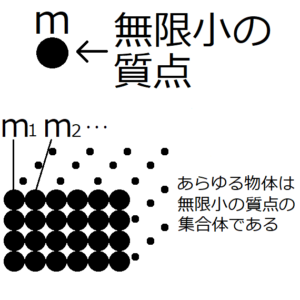
力を加えても変形しない物体を剛体という。そして、剛体は質点の集合体とみなすことができる。この記事では、剛体の運動方程式を導出してみる。
$$\displaystyle M\frac{d^2{\bf r}_G}{dt^2}=\sum_{i=1}^N {\bf F}_i$$
天秤から考える重心の意味と導出
[mathjax]
重心
$$ {\bf r}_G=\frac{\displaystyle \sum_{i=1}^N m_i{\bf r}_i}{\displaystyle \sum_{i=1}^N m_i }$$