量子力学の有名な原理として、不確定性原理がある。これは、粒子の正確な位置と運動量を同時に観測することはできないことを意味している。
この記事では、不確定性原理の意味の解説と、期待値を利用したものと不等式を利用したものの２通りの導出について、詳しく解説する。
波束と分散について
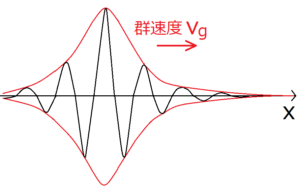
波束とは、限られた範囲にだけ存在する波のことをいう。高校までは主に全く同じ波形が無限に続くような波を考えてきたが、このような波は現実的でない。前の記事では波の重ね合わせによって生じるうなりによる群速度と位相速度について考えたが、それで学んだことは波束にも応用できる。
この記事では、古典力学の波動方程式に従う波束と、量子力学のシュレディンガー方程式に従う波束について考える。
参考:群速度と位相速度の導出
金属・絶縁体・半導体の違いとフェルミ準位について
電気伝導度の観点から物質を分類すると、金属・絶縁体・半導体に分けられる。これらの分類は、フェルミ準位の位置を意識することで簡単に分類できる。
この記事では、フェルミ準位の解説をしたあと、これらの分類についてバンドを用いて解説する。
バンドについて―価電子帯・禁制帯・伝導帯とはなにか
[mathjax]
固体物理や半導体の分野では、電子のエネルギー準位ごとの性質を考えるためにバンドという考えを導入する。
この記事では、バンドが何を表し、何に役に立つのかを考える。
なぜE=hνが成立するのか
$$E=hν$$
この式は、光の振動数\(ν\)とエネルギー\(E\)の関係式である。\(h\)はプランク定数で、次の定数となっている。
$$h≒6.63×10^{-34} [m^2kg/s]$$
この式は量子力学で最初に出てくる重要な公式であり、量子力学の勉強はここから始まると言っても過言ではない。電子のエネルギー準位が落ちたときには、その落ち幅に対応した振動数の光が放出されることになる。この式はその光の振動数の計算に非常に役に立つ。
この記事では、なぜ上の式が成立するのかを考える。
太陽光発電の仕組み
[mathjax]
再生可能エネルギーによる発電手段が注目される中、太陽光発電がその選択肢の一つとなっている。世界中のあちこちで大規模な太陽光パネルの設置工事が計画されており、主要な発電源となるのではと期待されている。
この記事では、太陽光パネルがどのような原理で電気を作り出すのかを書く。太陽光パネルにはpn接合型と色素増感太陽電池があるが、この記事ではpn接合型のものについて考える。
E=mc^2の意味とその導出
[mathjax]
$$E=mc^2$$
この式は、アインシュタインによって導かれた式として非常に有名である。Eはエネルギー、mは質量、cは光速度である。つまり、この式はエネルギーと質量の等価式だといえる。
この記事では、この式の導出と意味について考察する。
光電効果とは
[mathjax]
光電効果には、外部光電効果と内部光電効果と光起電力効果の3種類ある。アインシュタインがノーベル賞を受賞したきっかけとなった現象としても有名でもある。
この記事では、それぞれの光電効果の概要を述べる。
ブラッグの反射条件の導出とX線回折の原理について
[mathjax]
ブラッグの反射条件は次の式を指す。
$$λ=2d_{hkl}sinθ$$
d:実空間格子の(hkl)格子面の間隔 λ:光の波長 θ:格子面と入射光のなす角
上の式の(hkl)は、格子面のミラー指数である。
ブラッグの反射条件は、結晶によるX線回折を考えるときに使われる。この記事では、ブラッグ条件がX線回折にどうかかわってくるかや、XRDの仕組みについて書く。
トランジスタの仕組み―バイポーラとユニポーラの違い
トランジスタとは、スイッチング作用という特性を持つ半導体部品のことである。トランジスタは増幅回路でよく使われるため、もし電気回路について勉強するならば避けて通れないだろう。
この記事では、バイポーラトランジスタとユニポーラトランジスタの構造とその仕組みを、バンドを用いて説明する。